Giới thiệu MATLAB
MATLAB là phần mềm cung cấp môi trường tính toán số và lập trình, do công ty MathWorks thiết kế. MATLAB cho phép tính toán số với ma trận, vẽ đồ thị hàm số hay biểu đồ thông tin, thực hiện thuật toán, tạo các giao diện người dùng và liên kết với những chương trình máy tính viết trên nhiều ngôn ngữ lập trình khác.
Với thư viện Toolbox, MATLAB cho phép mô phỏng tính toán, thực nghiệm nhiều mô hình trong thực tế và kỹ thuật.
Lịch sử
Matlab là viết tắt từ “MATrix LABoratory”, được Cleve Moler phát minh vào cuối thập niên 1970, và sau đó là chủ nhiệm khoa máy tính tại Đại học New Mexico.
MATLAB, nguyên sơ được viết bởi ngôn ngữ Fortran, cho đến 1980 nó vẫn chỉ là một bộ phận được dùng nội bộ của Đại học Stanford.
Năm 1983, Jack Little, một người đã học ở MIT và Stanford, đã viết lại MATLAB bằng ngôn ngữ C và nó được xây dựng thêm các thư viện phục vụ cho thiết kế hệ thống điều khiển, hệ thống hộp công cụ (tool box), mô phỏng… Jack xây dựng MATLAB trở thành mô hình ngôn ngữ lập trình trên cơ sở ma trận (matrix-based programming language).
Steve Bangert là người đã viết trình thông dịch cho MATLAB. Công việc này kéo dài gần 1½ năm. Sau này, Jack Little kết hợp với Moler và Steve Bangert quyết định đưa MATLAB thành dự án thương mại – công ty The MathWorks ra đời thời gian này – năm 1984.
Phiên bản đầu tiên MATLAB 1.0 ra dời năm 1984 viết bằng C cho MS-DOS PC được phát hành đầu tiên tại IEEE Conference on Design and Control (Hội nghị IEEE về thiết kế và điều khiển) tại Las Vegas, Nevada. Ban đầu Matlab được phát triển để hỗ trợ sinh viên sử dụng hai thư viện LINPACK và EISPACK dùng cho đại số tuyến tính (viết bằng Fortran) mà không cần biết lập trình Fortran.
Năm 1986, MATLAB 2 ra đời trong đó hỗ trợ UNIX.
Năm 1987, MATLAB 3 phát hành.
Năm 1990 Simulink 1.0 được phát hành gói chung với MATLAB.
Năm 1992 MATLAB 4 thêm vào hỗ trợ 2-D và 3-D đồ họa màu và các ma trận truy tìm. Năm này cũng cho phát hành phiên bản MATLAB Student Edition (MATLAB ấn bản cho học sinh).
Năm 1993 MATLAB cho MS Windows ra đời. Đồng thời công ty này có trang web là www.mathworks.com
Năm 1995 MATLAB cho Linux ra đời. Trình dịch MATLAB có khả năng chuyển dịch từ ngôn ngữ MATLAB sang ngôn ngữ C cũng được phát hành trong dịp này.
Năm 1996 MATLAB 5 bao gồm thêm các kiểu dữ liệu, hình ảnh hóa, bộ truy sửa lỗi (debugger), và bộ tạo dựng GUI.
Năm 2000 MATLAB 6 cho đổi mới môi trường làm việc MATLAB, thay thế LINPACK và EISPACK bằng LAPACK và BLAS.[2]
Năm 2002 MATLAB 6.5 phát hành đã cải thiện tốc độ tính toán, sử dụng phương pháp dịch JIT (Just in Time) và tái hỗ trợ MAC.
Năm 2004 MATLAB 7 phát hành, có khả năng chính xác đơn và kiểu nguyên, hỗ trợ hàm lồng nhau, công cụ vẽ điểm, và có môi trường phân tích số liệu tương tác.
Đến tháng 12, 2008, phiên bản 7.7 được phát hành với SP3 cải thiện Simulink cùng với hơn 75 sản phẩm khác.
Năm 2009 cho ra đời 2 phiên bản 7.8 (R2009a) và 7.9 (R2009b).
Năm 2010 phiên bản 7.10 (R2010a) cũng đã được phát hành.
Năm 2019 phiên bản 9.6 (R2019a) cũng đã được phát hành.
Matlab được dùng rộng rãi trong giáo dục, phổ biến nhất là giải các bài toán số trị (cả đại số tuyến tính lẫn giải tích) trong nhiều lĩnh vực kĩ thuật.
Cài đặt Matlab
Thiết Lập Môi Trường Matlab
Yêu cầu phần cứng
Yêu cầu cấu hình hệ thống phiên bản Matlab 2019a đối với hệ điều hành Windows:
Hỗ trợ các hệ điều hành
- Windows 10
- Windows 7 Service Pack 1
- Windows Server 2019
- Windows Server 2016
Ghi chú:
- Windows Server 2019 không hỗ trợ phiên bản R2019a.
- Windows Server 2012 and Windows Server 2012 R2 không hỗ trợ phiên bản R2019a.
Bộ vi xử lý:
- Tối thiếu: Bộ vi xử lý Intel hoặc AMD x86-64
- Khuyến nghị: Bộ vi xử lý AMD x86-64 4 lõi trở lên và hỗ trợ chuẩn AVX2
Ổ địa cứng (HDD):
- Tối thiểu: 2.9 GB khoảng chống HDD cho MATLAB, 5-8 GB phục vụ cài đặt
- Khuyến nghị: Nên sử dụng ổ cứng dạng rắn (SSD)
- Cài toàn bộ tính năng của Matlab cần 29 GB ổ cứng
RAM:
- Tối thiểu: 4 GB
- Khuyến nghị: 8 GB
- Đối với Polyspace cần 4 GB trên 1 lõi CPU
Đồ họa (Graphics):
- Không cần card rời.
- Card đồ họa cần hỗ trợ OpenGL 3.3 với 1GB GPU bộ nhớ.
Các bước cài đặt
Bước 1: Tải về MATLAB R2019a
Bước 2: Sau khi tải phiên bản Matlab R2019a về máy, ta mở thư mục cài đặt để tiến hành cài đặt.
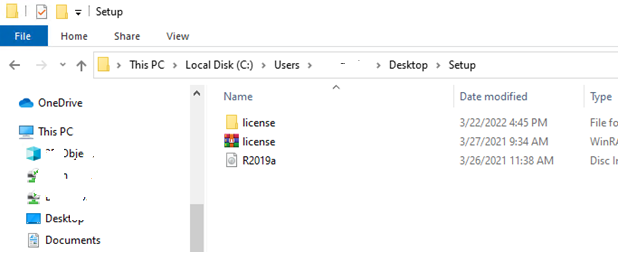
Màn hình 1: Cấu trúc thư mục cài đặt
Bước 3: Mở file R2019a.iso (có thể dùng trình explore mặc định của Windows hoặc các công cụ có hỗ trợ mở tệp “.iso”)
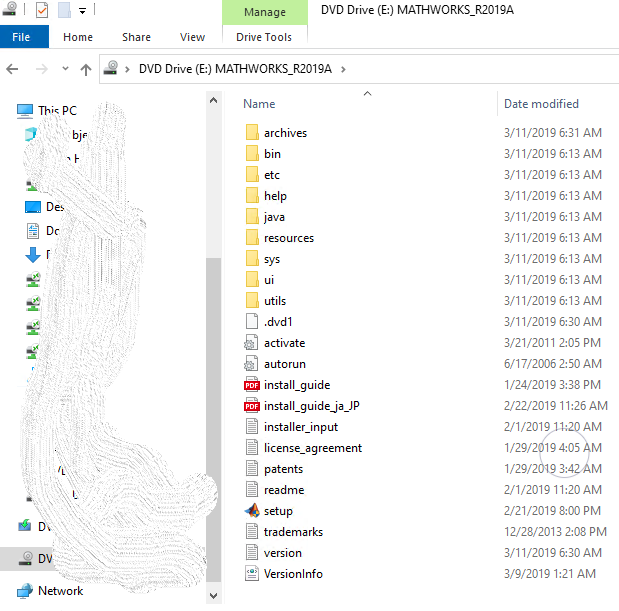
Màn hình 2: Cấu trúc thư mục của tệp R2019a.iso
Bước 4: Click đúp chuột vào tệp setup.exe để tiến hành cài đặt Matlab phiên bản 9.6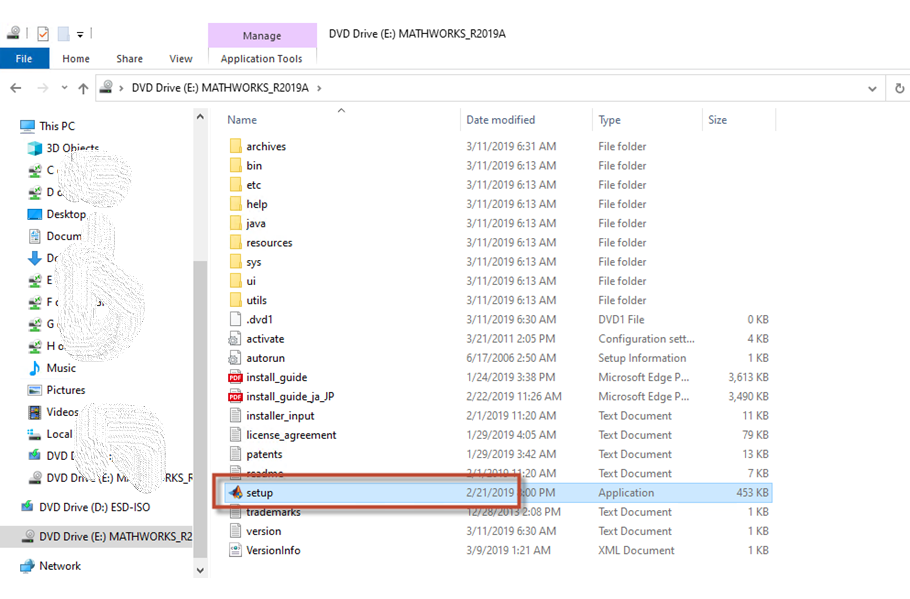 
Màn hình 3: Vị trí tệp setup.exe
Bước 5: Sau khi click đúp vào tệp setup.exe, bộ cài sẽ được giải nén vào thự mục tạm của hệ điều hành Windows và thực thi tiến trình cài đặt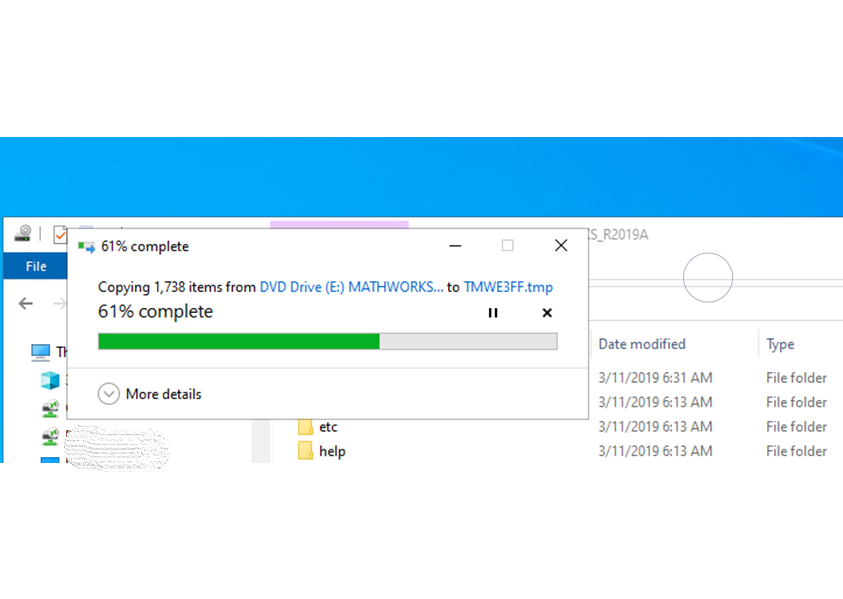
Màn hình 4: Bộ cài đặt đang được giải nén
Bước 6: Lựa chọn phương thức cài đặt, có thể cài đặt qua tài khoản đã đăng ký với MathWorks hoặc cài đặt qua key cài đặt. Ở đây, ta chọn cài đặt qua key như hình vẽ và bấm vào nút “Next” để qua màn hình cài đặt tiếp theo.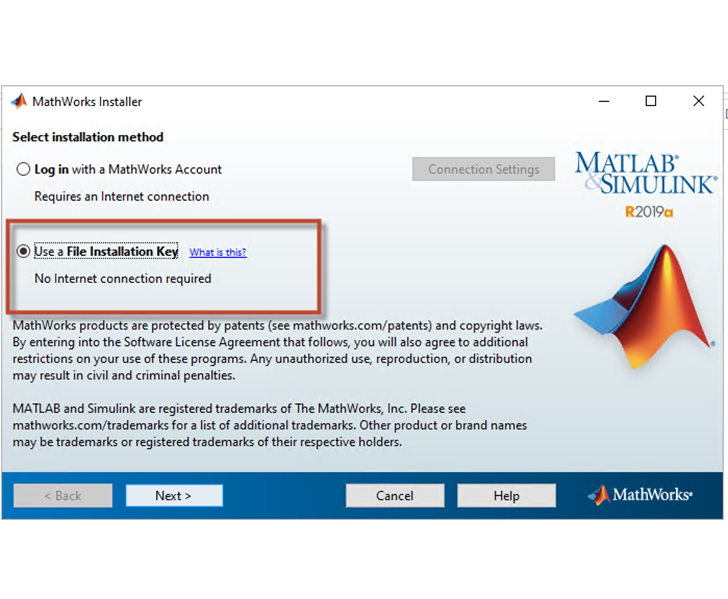 
Màn hình 5: Lựa chọn phương thức cài đặt
Bước 7: Xác nhận thỏa thuận cấp phép “License Agreement”, ta chọn “Yes” và bấm vào nút “Next” để qua màn hình cài đặt tiếp theo.
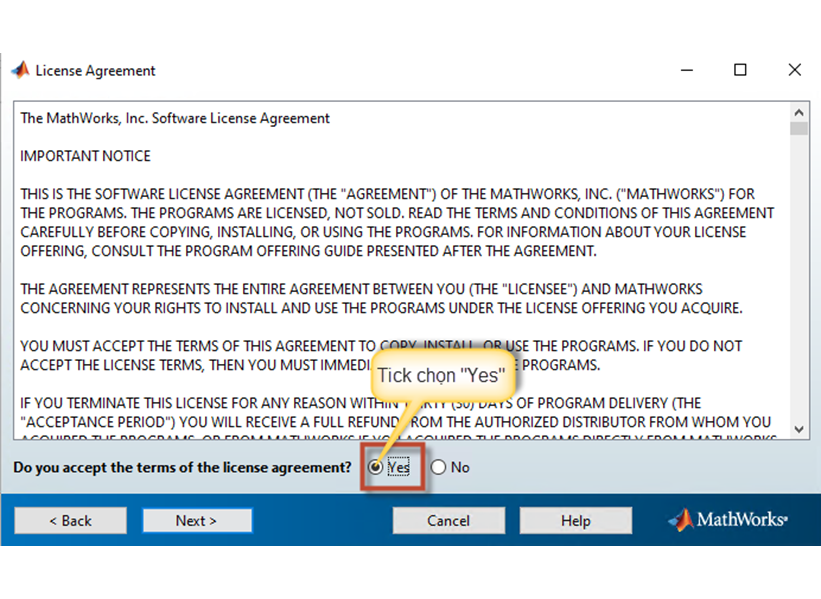
Màn hình 6: Xác nhận thỏa thuận cấp phép
Bước 8: Trình cài đặt hiển thị màn hình nhập key cài đặt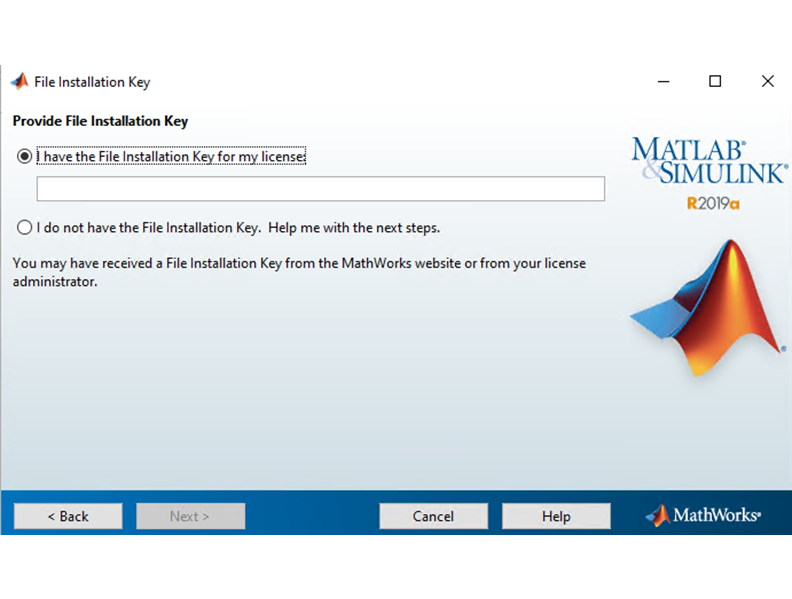
Màn hình 7: màn hình key cài đặt
Bước 9: Nhập key cài đặt và bấm vào nút “Next” để qua màn hình cài đặt tiếp theo.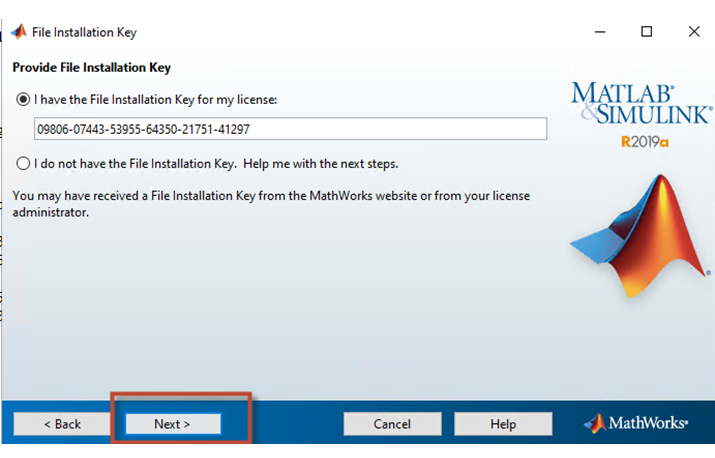 
Màn hình 8: Màn hình nhập key cài đặt
Bước 10: Lựa chọn thư mục cài đặt, nếu có nhu cầu thay đổi thư mục cài đặt thì ta bấm nút “Browse” để lựa chọn sang thư mục khác. Ở đây, ta chọn mặc định và bấm nút “Next” để qua màn hình cài đặt tiếp theo.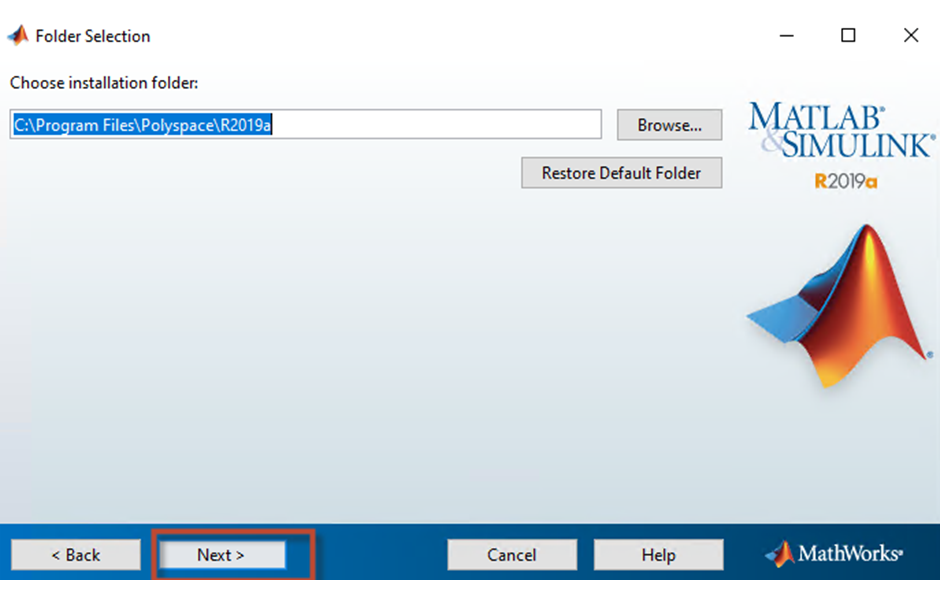
Màn hình 9: Lựa chọn thư mục cài đặt
Bước 11: Lựa chọn các sản phẩm/chức năng của hệ thống Matlab phiên bản 9.6 cần cài đặt, nếu cần tiết kiệm bộ nhớ thì ta chỉ cần chọn nhưng sản phẩm/chức năng mà ta thực sự cần (lựa chọn ở khoanh vùng màu xanh) và bấm nút “Next” để qua màn hình cài đặt tiếp theo.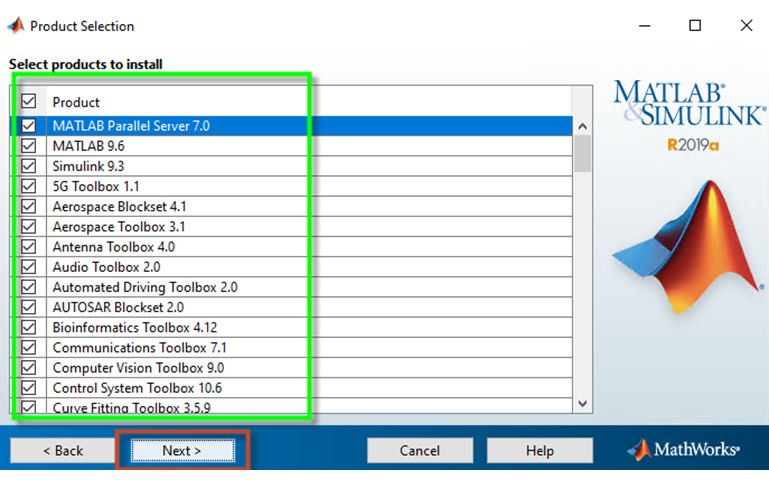
Màn hình 10: Lựa chọn sản phẩm/chức năng
Bước 12: Lựa chọn tạo shortcut phục vụ truy cập sau khi hệ thống cài đặt xong (có thể lựa chọn ở desktop hoặc start menu, ở đây ta để mặc định) và bấm nút “Next” để bắt đầu tiến trình cài đặt.
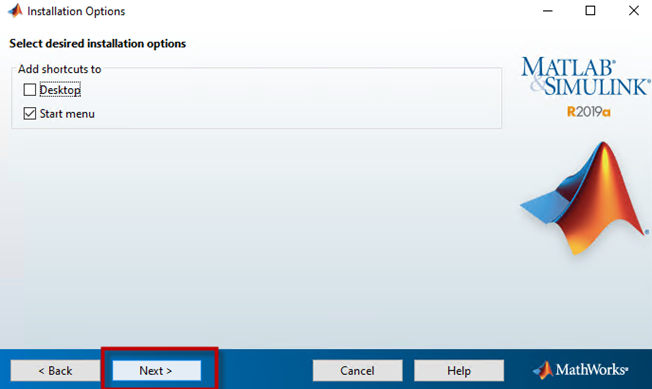
Màn hình 11: Lựa chọn tạo shortcut
Bước 13: Tiến trình cài đặt bắt đầu, ta đợi cho tiến trình thực hiện cài đặt các sản phẩm/chức năng mà ta đã chọn. Tùy theo cầu hình của máy tính, tiến trình này có thế mất 20p hoặc lâu hơn.
Màn hình 12: Cài đặt Parallel Server 7.0
Màn hình 13: Cài đặt Simulink 9.3
Màn hình 14: Cài đặt Bioinformatics Toolbox 4.12
Màn hình 15: Cài đặt Matlab
Bước 14: Sau khi cài đặt các sản phẩm/chức năng, tiến trình cài đặt hiển thị danh sách các ghi chú về cấu hình cài đặt, ta bấm “Next” để qua màn hình cài đặt tiếp theo.
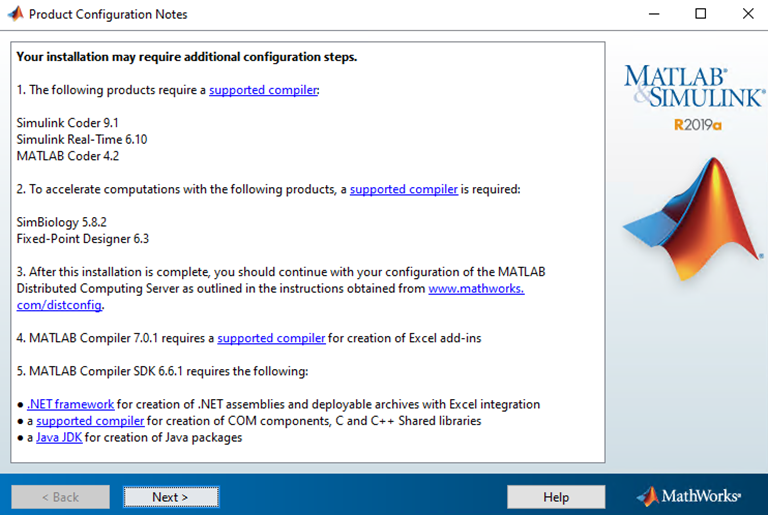Màn hình 16: Màn hình danh sách ghi chú về cấu hình cài đặt
Bước 15: Sau khi hiện thị danh sách ghi chú về cấu hình cài đặt, tiến trình cài đặt kết thúc, ta bấm nút “Finish” để hoàn thành tiến trình cài đặt.
Màn hình 17: Tiến trình cài đặt kết thúc
Bước 16: Kích hoạt bản quyền đã mua, bằng cách chạy Polyspace R2019 từ Start menu.
Màn hình18: Chạy Polyspace từ Start menu
Bước 17: Hệ thống Matlab sẽ hiện thị lên giao diện kích hoạt bản quyền, ta chọn “Active manually without the Internet” và bấm “Next” để qua bước kích hoạt tiếp theo.
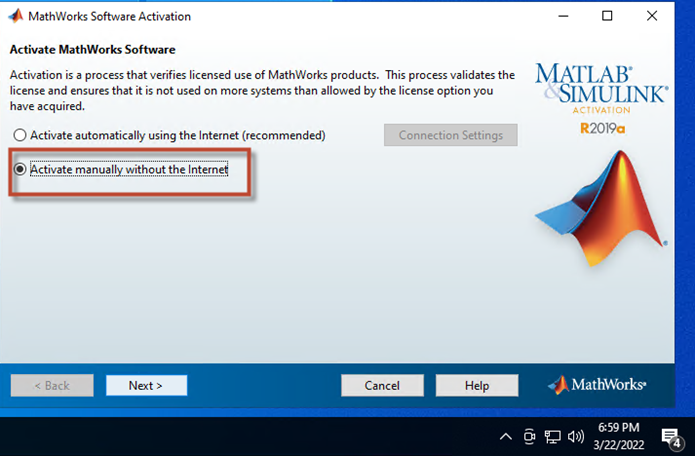
Màn hình 19: Lựa chọn phương thức kích hoạt bản quyền
Bước 18: Lựa chọn phải bản quyền được cấp bằng cách bấm vào nút “Browse” sau đó bấm nút “Next” để hoàn tất.
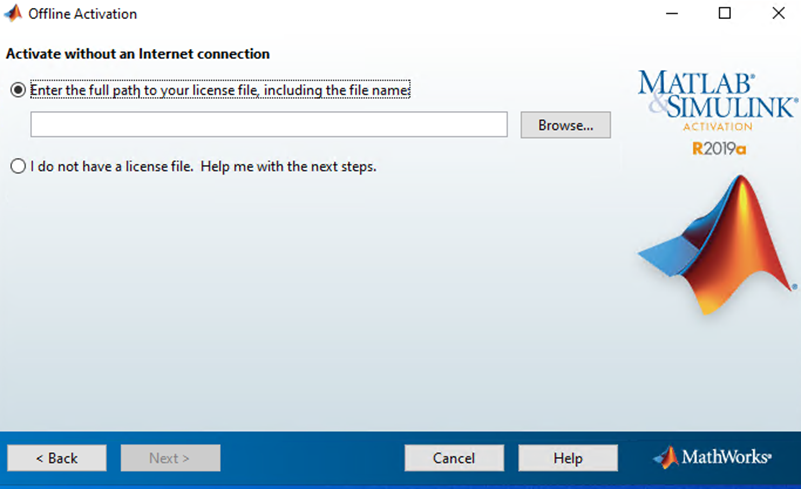
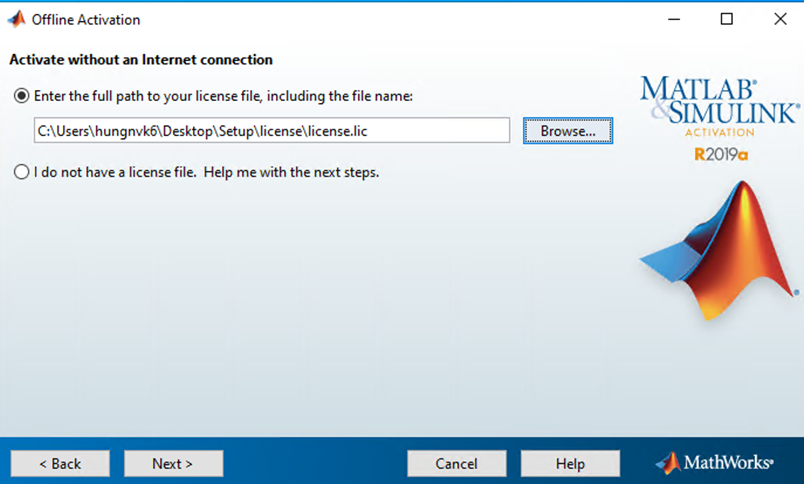
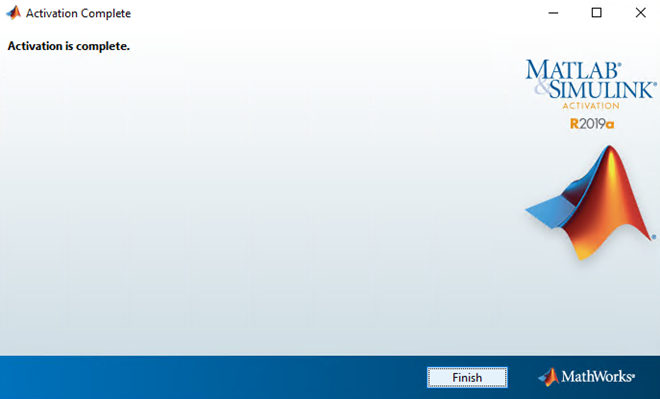
Bước 19: Bấm nút “Finish” để kết thúc quá trình kích hoạt bản quyền.
Làm Quen Với Môi Trường Matlab
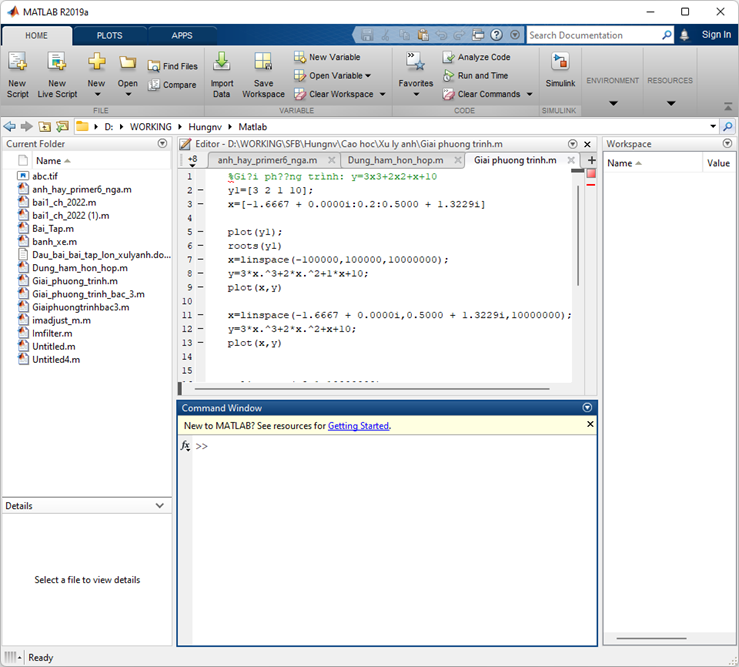
Matlab phát triển IDE (môi trường phát triển tích hợp) có thể khởi chạy từ biểu tượng được tạo trên màn hình desktop. Cửa sổ làm việc chính trên Matlab được gọi là desktop. Khi Matlab bắt đầu chạy, desktop sẽ hiển thị trong các layout mặc định:
Current Folder: Bảng này cho phép người dùng truy cập thư mục và các file của dự án.
– Command Window: Đây là khu vực chính, nơi mà các lệnh được nhập vào tiện ích dòng lệnh. Cửa sổ này được nhận diện bởi dấu nhắc lệnh (>>).
Workspace : Workspace hiển thị tất cả các biến tạo ra hoặc nhập từ các file.
Command History: Bảng này hiển thị hoặc trả về lệnh được nhập trên tiện ích dòng lệnh.
CHƯƠNG 2: LÀM TÍNH CHO CÁC MẢNG
Tất cả các biến trong matlab là mảng nhiều chiều, không kể đó là loại dữ liệu nào (từ số đến chuỗi kí tự)
Tạo mảng Array
Để tạo mảng có 4 phần tử trên 1 hàng dùng nhập các phần tử trong dấu ngoặc vuông [], phân biệt các phần tử bằng dấu cách hoặc dấu phẩy (,). Ví dụ mảng 1 chiều a (đây cũng gọi là vector hàng):
a = [1 2 3 4]
a =
1 2 3 4
Để tạo ma trận có nhiều hàng các hàng được phân biệt bằng dấu chấm phẩy (;).
Cách khác để tạo 1 ma trận đó là sử dụng hàm có sẵn như hàm ones, zeros, hoặc rand. Tuy nhiên các hàm này tạo ra giá trị mặc định (trừ hàm rand). Ví dụ, tạo 1 ma trận 5 hàng 1 cột gồm các phần tử 0:
z = zeros(5,1)
z =
0
0
0
0
0
a = [1 2 3; 4 5 6; 7 8 10]
a =
1 2 3
4 5 6
7 8 10
Mục lục bài viết
Các phép toán đối với Ma trận và Mảng
MATLAB cho phép người dùng thực hiện các toán tử đại số cho 1 phần tử đối với tất cả các phần tử của ma trận và mảng. Ví dụ:
a + 10
ans =
11 12 13
14 15 16
17 18 20
sin(a)
ans =
0.8415 0.9093 0.1411
-0.7568 -0.9589 -0.2794
0.6570 0.9894 -0.5440
Để chuyển vị một ma trận người ta dùng dấu (‘). Ví dụ:
a’
ans =
1 4 7
2 5 8
3 6 10
Có thể thực hiện phép nhân ma trận bằng toán tử nhân (*) nhưng phải tuân theo quy tắc nhân ma trận. Ví dụ ma trận a có thể nhân với ma trận đảo của nó và cho ra ma trận đơn vị (a là ma trận vuông)
p = a*inv(a)
p =
1.0000 0 -0.0000
0 1.0000 0
0 0 1.0000
Trong ví dụ trên p không phải là ma trận có các phần tử nguyên (integer). MATLAB lưu các giá trị số dưới dạng dữ liệu có dấu phẩy động. Có thể thay đổi và hiển thị ra nhiều giá trị thập phân sau dấu phẩy hơn bằng cách sử dụng câu lệnh format:
format long
p = a*inv(a)
p =
1.000000000000000 0 -0.000000000000000
0 1.000000000000000 0
0 0 0.999999999999998
Để thiết lập lại định dạng cũ ta có thể dùng câu lệnh:
format short
Định dạng chỉ làm thay đổi cách thể hiện các số ra màn hình chứ thông thay đổi cách mà Matlab lưu trức các giá trị đó.
Để tác động toán tử nhân lên từng phần tử trong ma trận người dùng phải dùng toán tử .*
p = a.*a
p =
1 4 9
16 25 36
49 64 100
Phép chia và hàm mũ. Để tác động lên từng phần tử phải sử dụng dấu chấm (.)
a.^3
ans =
1 8 27
64 125 216
343 512 1000
Toán tử ghép (Concatenation)
Toán tử này thực hiện nối các mảng với nhau và tạo nên mảng lớn hơn. Dấu ngoặc vuông [] chính là toán tử này.
Ví dụ:
A = [a,a]
A =
1 2 3 1 2 3
4 5 6 4 5 6
Có thể thực hiện nối theo phương ngang (hàng) hoặc theo phương dọc (cột) bằng cách không hoặc có sử dụng dấu chấm phẩy (;).
Ví dụ:
A = [a; a]
A =
1 2 3
4 5 6
7 8 10
1 2 3
4 5 6
7 8 10
Số phức
Số phức có phần thực và phần ảo (bình phương phần ảo là –1)
sqrt(-1)
ans =
0.0000 + 1.0000i
Để thể hiện phần ảo, ta dùng sử dụng kí hiệu i hoặc j.
c = [3+4i, 4+3j; -i, 10j]
c =
3.0000 + 4.0000i 4.0000 + 3.0000i
0.0000 – 1.0000i 0.0000 +10.0000i
Vẽ đồ thị 2D
Để vẽ đồ thì 2D dạng đường người dùng sử dụng hàm plot.
Ví dụ vẽ đồ thị hàm sin() nằm trong khoảng từ 0 đến 2*pi
x = 0:pi/100:2*pi;
y = sin(x);
plot(x,y)
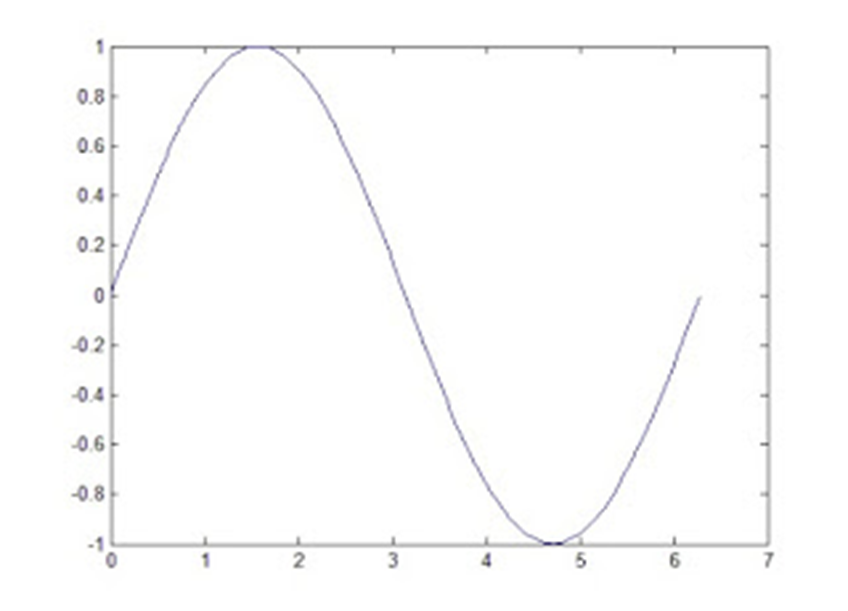
Có thể gán nhãn cho các trục bằng cách sử dụng lệnh:
xlabel(‘x’)
ylabel(‘sin(x)’)
title(‘Vẽ đồ thị hình sin’)
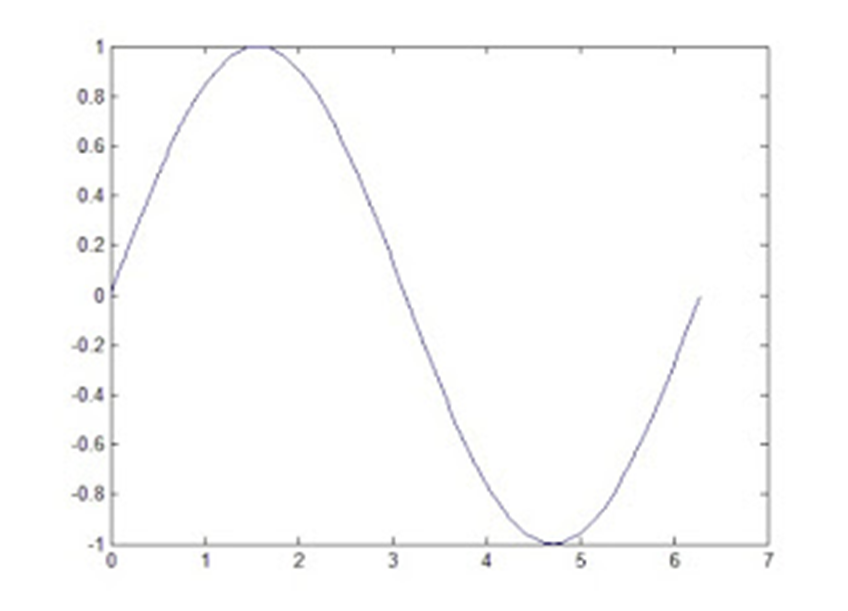
Đưa thêm đầu vào cho hàm plot, cũng có thể thay đổi nét vẽ sang nét đứt màu đỏ:
plot(x,y,’r–‘)
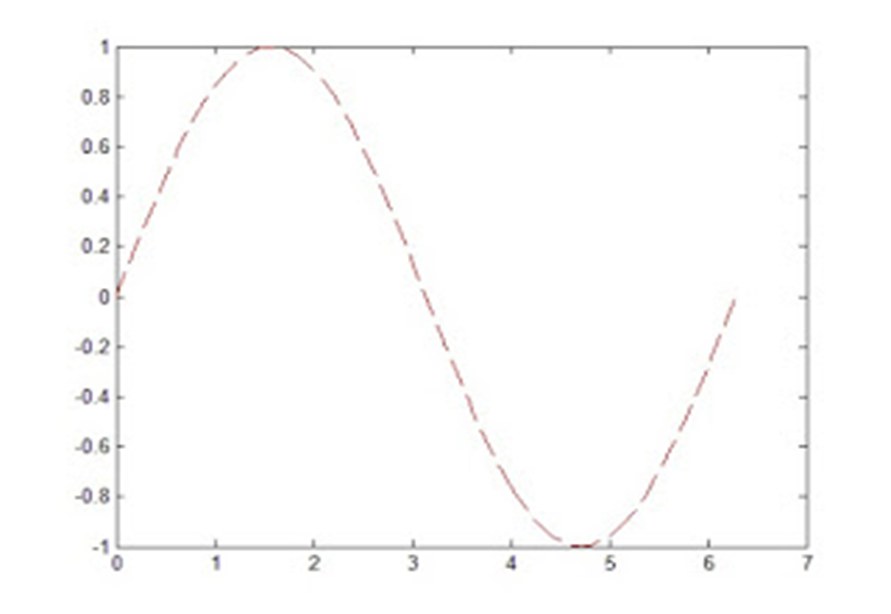
Cụm kí tự ‘r–‘ là một sự chỉ định dạng đồ thị. Mỗi cụm kí tự chỉ định có thể bao gồm các kí tự nhằm thay đổi màu sắc, kiểu cách, và làm chỉ thị. Một chỉ thị marker là một kí hiệu xuất hiện tại mỗi điểm dữ liệu, ví dụ như +, o, *. Ví dụ ‘g:*’ sẽ hiển thị đồ thị dưới dạng chấm và chỉ thị hình * .
Để thêm một đồ thị hàm số khác vào cùng với đồ thị hiện tại phải sử dụng hàm hold on
x = 0:pi/100:2*pi;
y = sin(x);
plot(x,y)
hold on
y2 = cos(x);
plot(x,y2,’r:’)
legend(‘sin’,’cos’)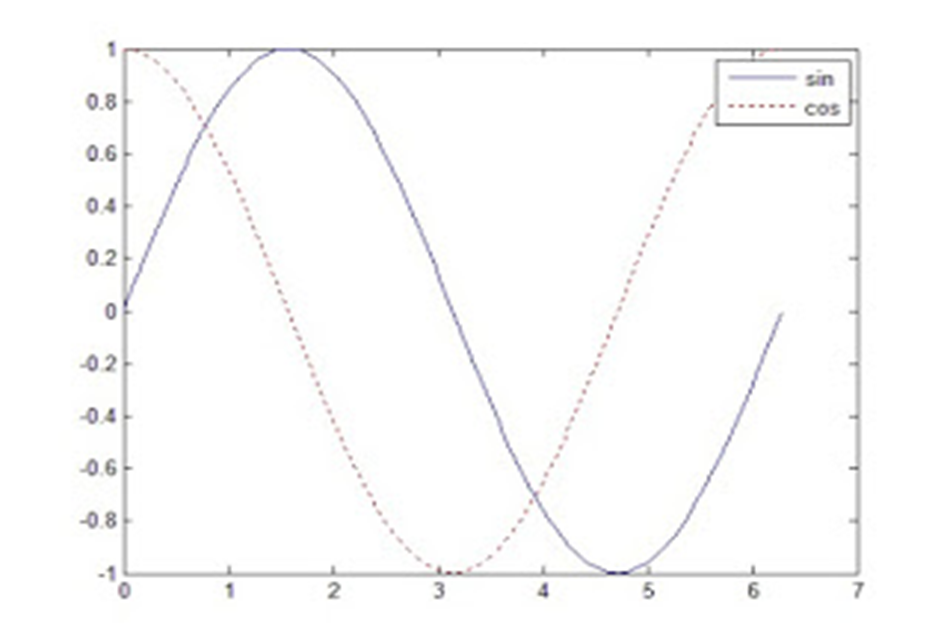 
Vẽ đồ thị 3D
Đồ thị 3D thể hiện mặt được thể hiện dưới dạng hàm như sau : z = f(x,y) .
Để đánh giá z, đầu tiên chúng ta tạo ra tập điểm (x,y) trên miền chỉ định bằng cách sử dụng hàmmeshgrid.
[X,Y] = meshgrid(-2:.2:2);
Z = X .* exp(-X.^2 – Y.^2);
Sau đó vẽ đồ thị 3D bằng hàm surf
surf(X,Y,Z)
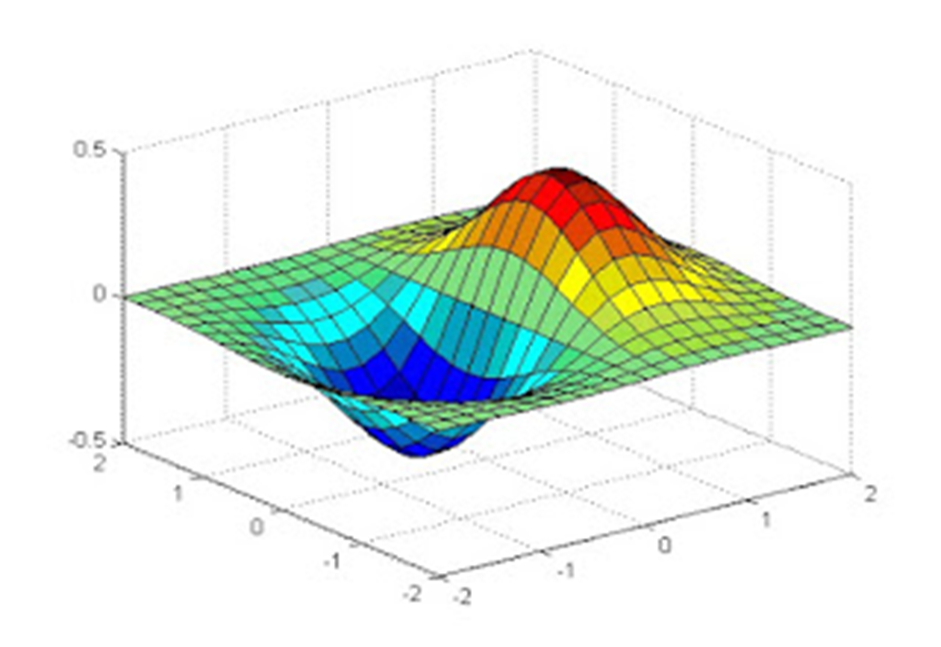
Đồ thị con Có thể hiển thị nhiều đồ thị trên khung đồ thị con bằng cách sử dụng hàm subplot
Ví dụ g ta có 4 khung đồ thị con trong một khung đồ thị chính.
t = 0:pi/10:2*pi;
[X,Y,Z] = cylinder(4*cos(t));
subplot(2,2,1); mesh(X); title(‘X’);
subplot(2,2,2); mesh(Y); title(‘Y’);
subplot(2,2,3); mesh(Z); title(‘Z’);
subplot(2,2,4); mesh(X,Y,Z); title(‘X,Y,Z’);
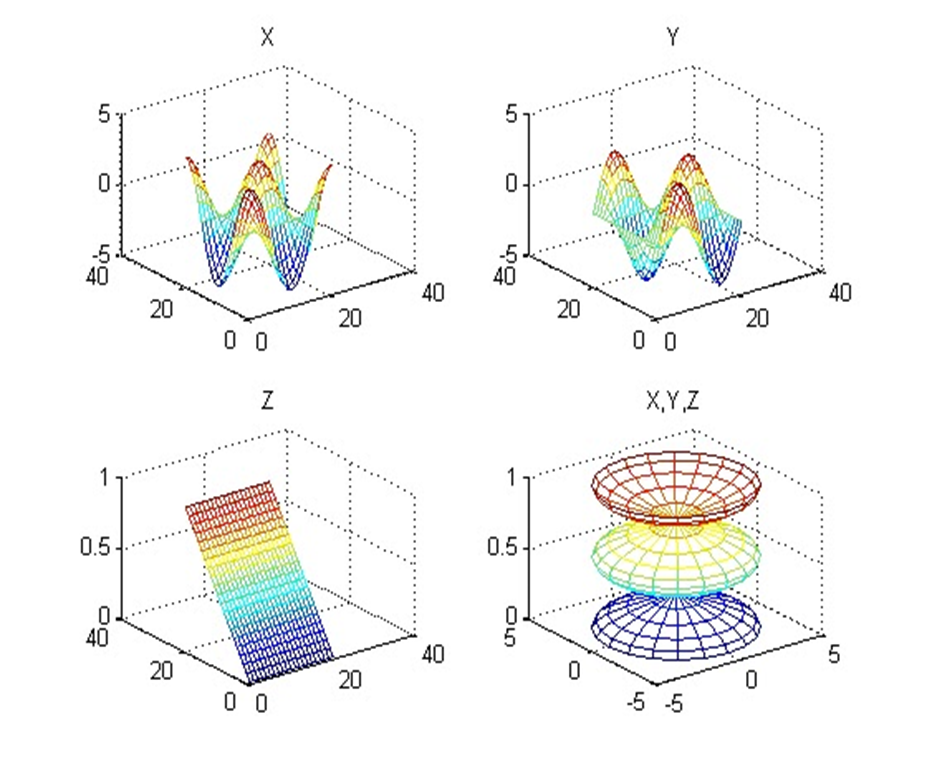
CHƯƠNG 3: XỬ LÝ ẢNH TRONG MATLAB
Matlab là một ngôn ngữ rất mạnh và hỗ trợ rất tốt các thao tác làm việc trên ảnh. Vì vậy việc sử dụng matlab cho các ứng dụng xử lý ảnh gần như là lựa chọn hàng đầu cho những ai muốn thực hiện các thuật toán xử lý trên phần mềm. Một số hàm cơ bản dùng để xử lý ảnh trong matlab:
Hàm imread()
– Lệnh imread() sẽ đọc một file thành một ma trận. Matlab trợ giúp rất nhiều định dạng đồ hoạ thông dụng chẳng hạn: BMP, GIF, JPEG, PNG, TIFF …
Ví dụ file ảnh: file ảnh cho bạn nào cần : erkeleyTower.png
>> img = imread(‘ImageProcessing_1/BerkeleyTower.png’);
>> size(img)
ans =
499 748 3
– Ví dụ trên chúng ta khi đọc một file ảnh bằng imread sẽ có kết quả là một ma trận 499×748 với 3 thành phần màu cơ bản RGB . Các ma trận như sau:
Lệnh code:
24 40 73 108 129 108 96 100 109 114 108 109 62
29 56 97 107 110 104 103 105 106 110 110 111 105
…
3 2 2 1 0 0 1 1 0 1 2 4 2
1 0 1 3 2 0 0 0 1 1 2 1 0
…
Hàm imshow() và imagesc()
– Để hiển thị hình ảnh trong matlab ta dùng 2 lệnh sau imshow và imagesc. Lệnh imshow cho chúng ta một hình ảnh trong định dạng tiêu chuẩn là 8-bit, giống như trong một trình duyệt web. Lệnh imagesc hiển thị các hình ảnh trên các trục đồ thị với giá trị min là màu đen và giá trị tối đa là màu trắng.
Lệnh code:
img = imread(‘ImageProcessing_1/BerkeleyTower.png’);
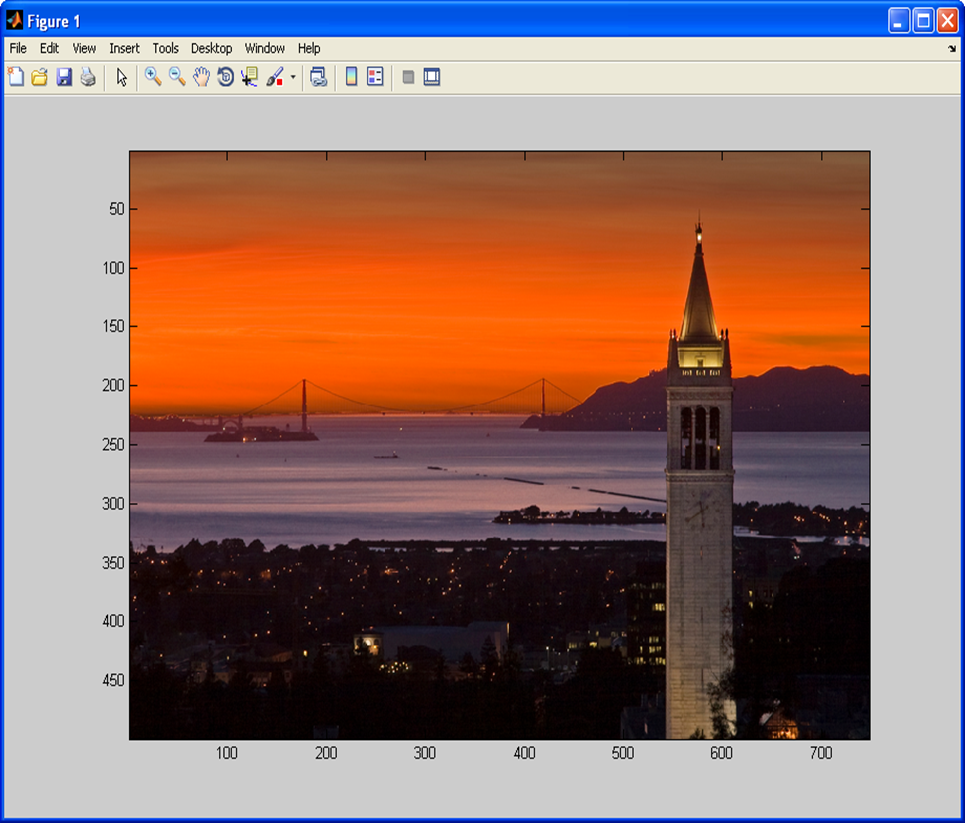
imshow(img);
imagesc(img);
Dùng imshow
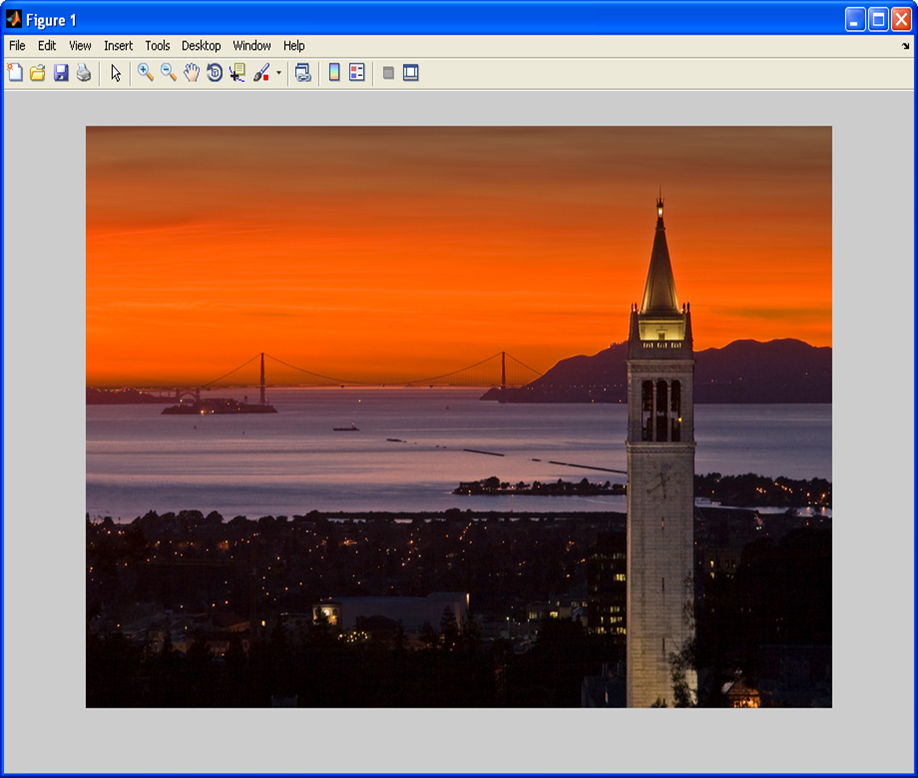
Dùng lệnh imagesc
Có thể kiểm tra giá trị RGB với (x,y) là tọa độ một điểm ảnh:
Chọn “Data Cursor” trên thanh công cụ.
Nhấn vào bất kì điểm nào ta sẽ có giá trị của từng điểm đó.
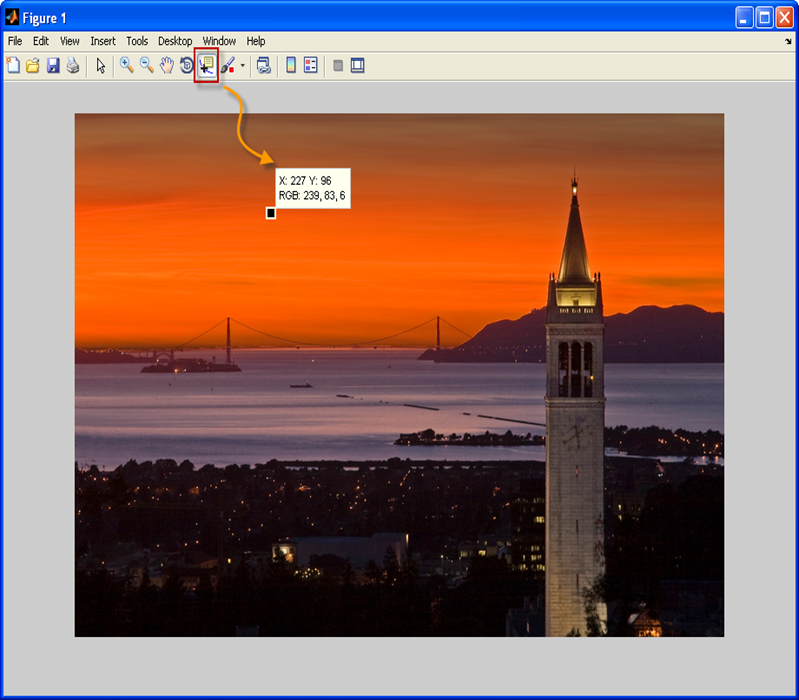
Mỗi điểm ảnh là một vector 3 chiều với các giá trị trong khoảng [0-255]. 3 thông số hiển thị là giá trị của RGB.
mỗi một hình ảnh là một hình ảnh kết hợp của 3 màu RGB. Vì vậy, có thể hiển thị các thành phần RGB riêng của hình ảnh bằng cách sử dụng các lệnh sau đây:
Lệnh code:
subplot(131);
imagesc(img(:,:,1));
title(‘Red’);
subplot(132);
imagesc(img(:,:,2));
title(‘Green’);
subplot(133);
imagesc(img(:,:,3));
title(‘Blue’);
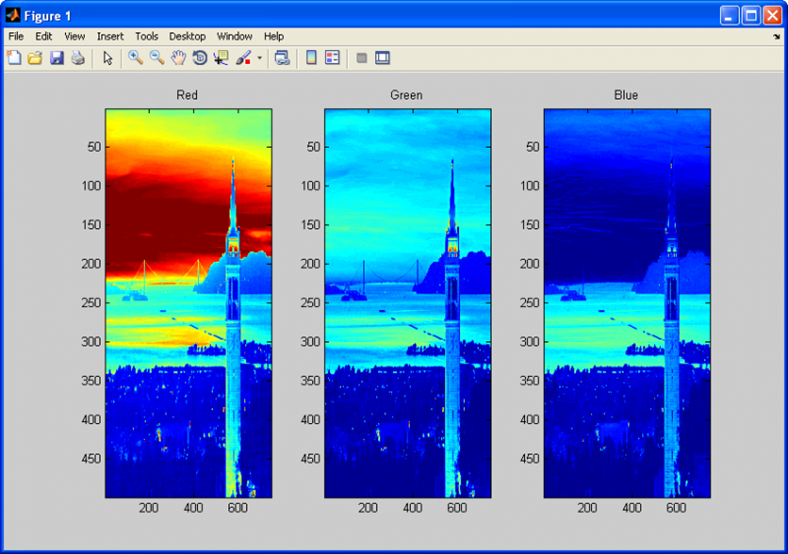
– Câu lệnh : colormap gray , làm cho tất các hình ảnh chuyển thành màu xám.
Hàm imwrite
– Để lưu một ảnh sử dụng câu lệnh imwrite(). Cấu trúc cơ bản nhất của imwrite() sẽ yêu cầu một biến ảnh và tên file. Nếugộp một phần mở rộng trong tên file,Matlab sẽ nhận ra định dạng mong muốn từ nó- Để lưu một ảnh, chúng ta sử dụng câu lệnh imwrite(). Cấu trúc cơ bản nhất của imwrite() sẽ yêu cầu một biến ảnh và tên file. Nếu ta gộp một phần mở rộng trong tên file, Matlab sẽ nhận ra định dạng mong muốn từ nó.
imwrite(blue_img, ‘Blue4_BerkeleyTower.png’, ‘png’);
Xem nhiều ảnh
– Nếu ta chỉ ra một file mà chứa nhiều ảnh, hàm imview chỉ hiển thị ảnh đầu tiên trong file đó. Để xem tất cả các ảnh trong file, sử dụng hàm imread để nhập mỗi ảnh vào trong không gian làm việc của Matlab sau đó gọi hàm imview nhiều lần để hiển thị mỗi ảnh riêng biệt.
Hàm rgb2gray()
img = imread(‘ImageProcessing_1/BerkeleyTower.png’);
gray = rgb2gray(img);
imshow(gray);
>> size(gray)
ans = 499 748
– Lệnh(rgb2gray) chuyển đổi hình ảnh RGB thành trắng đen bằng cách loại bỏ các thông tin màu sắc và độ bão hòa nhưng vẫn giữ độ sáng.
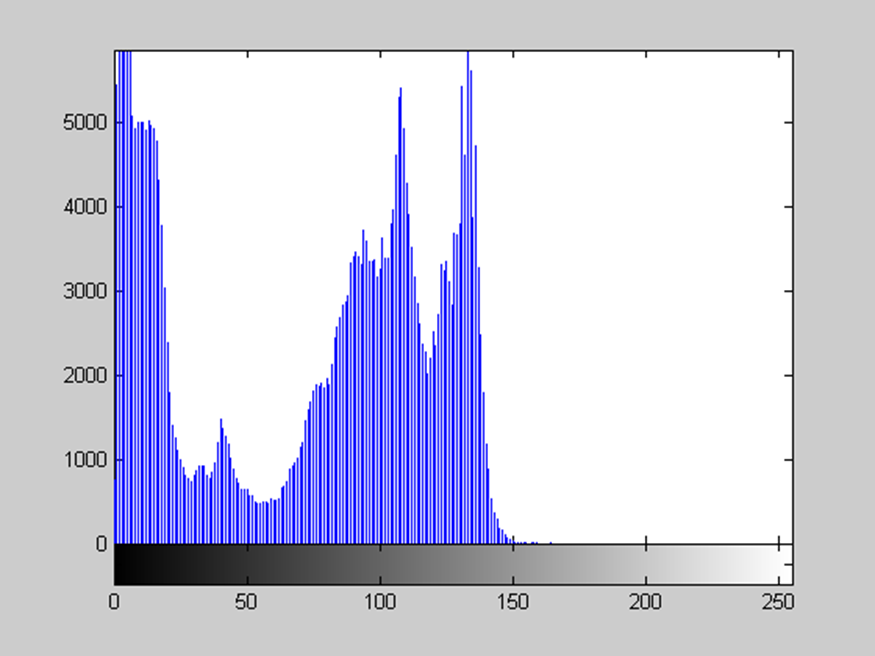
Hàm imhist
– Hiển thị một biểu đồ của dữ liệu hình ảnh. imhist(img, n) sẽ hiển thị một biểu đồ với n bins cho cường độ hình ảnh trên một colorbar grayscale có độ dài n. Nếu bỏ qua tham số, imhist() sử dụng một giá trị mặc định n = 256 nếu là một hình ảnh grayscale, hoặc n = 2 nếu là một hình ảnh nhị phân.
img = imread(‘ImageProcessing_1/BerkeleyTower.png’);
gray = rgb2gray(img);
imhist(gray);
Hàm imadjust()
– imadjust() điều chỉnh giá trị cường độ hình ảnh. Câu lệnh này làm tăng độ tương phản của hình ảnh đầu ra.File ẢNH : Rachmaninoff.jpg.
img = imread(‘ImageProcessing_1/Rachmaninoff.jpg’);
gray = rgb2gray(img);
adj_img = imadjust(gray, [0.3,0.7],[]);
subplot(121);
imshow(gray);
title(‘input image’);
subplot(122);
imshow(adj_img);
title(‘Binary image’);
Độ tương phản của ảnh
Phép nhân và chia được sử dụng như một phương thức đơn giản điều chỉnh độ tương phản và là phần mở rộng của phép cộng và trừ (ví dụ giảm độ tương phản đến 25% chia cho 4; tăng độ tương phản 50% nhân 1,5). Quá trình này đôi khi được gọi là chia tỉ lệ màu sắc hình hảnh
Phép chia có thể được sử dụng cho Differencing(vi phân) hình ảnh, ví dụ chia một hình ảnh với một hình ảnh khác cho kết quả là 1.0 nếu các giá trị điểm ảnh giống hệt nhau và giá trị khác 1.0 mà sự khác biệt xảy ra. Tuy nhiên, Differencing hình ảnh sử dụng phép trừ được tính toán hiệu quả hơn. Chia và nhân 2 hình ảnh khác nhau thường không được sử dụng nhiều trong xử lý ảnh.
– Code matlab:
A=imread(‘peppers.png’); % Read in 1st image
subplot(1,3,1), imshow(A); % Display 1st image
title(‘anh 1’);
Output1 = immultiply(A,1.5); % multiple image by 1.5
subplot(1,3,2), imshow(Output1); % Display result
title(‘anh out1’);
Output2 = imdivide(A,4); % divide image by 4
subplot(1,3,3), imshow(Output2); % Display result
title(‘anh out2’);
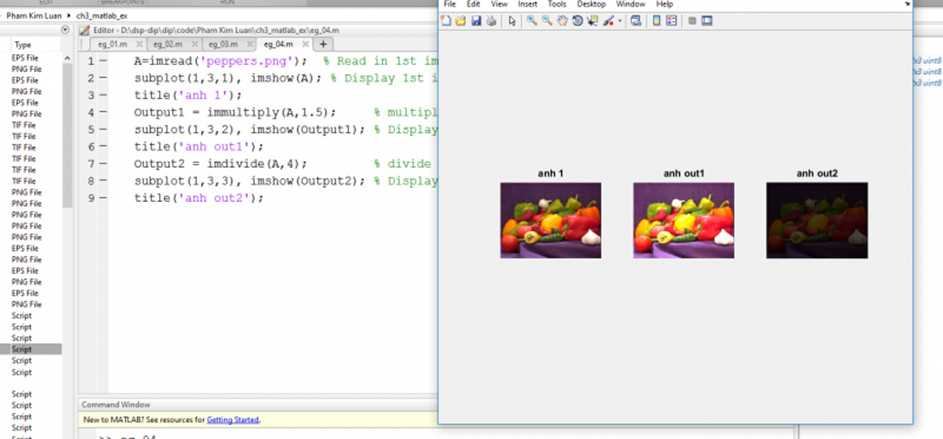
– Đối với tất cả các phép tính số học giữa các hình ảnh chúng ta phải đảm bảo rằng các giá trị điểm ảnh có kết quả vẫn nằm trong phạm vi số nguyên hiện có sẵn của các kiểu dữ liệu / kích thước. Ví dụ, một hình ảnh 8-bit biểu diễn cho 256 giá trị trong mỗi vị trí pixel. Nếu giá trị điểm ảnh không nằm trong phạm vi cho phép từ 0-255 thì tràn số nguyên sẽ xảy ra và giá trị sẽ thường ‘wrap around’ một giá trị thấp. Điều này thường được gọi là bão hòa trong không gian ảnh: giá trị vượt quá khả năng biểu hiện của hình ảnh. Một giải pháp là để phát hiện tràn và tránh nó bằng cách thiết lập các giá trị với giá trị tối đa cho các biểu diễn hình ảnh (ví dụ cắt ngắn đến 255). Phương pháp xử lý tràn được thực hiện trong imadd, imsubtract, immultiply và imdivide. Đối với ba kênh hình ảnh RGB các phép toán toán học thường được thực hiện riêng cho từng kênh màu.
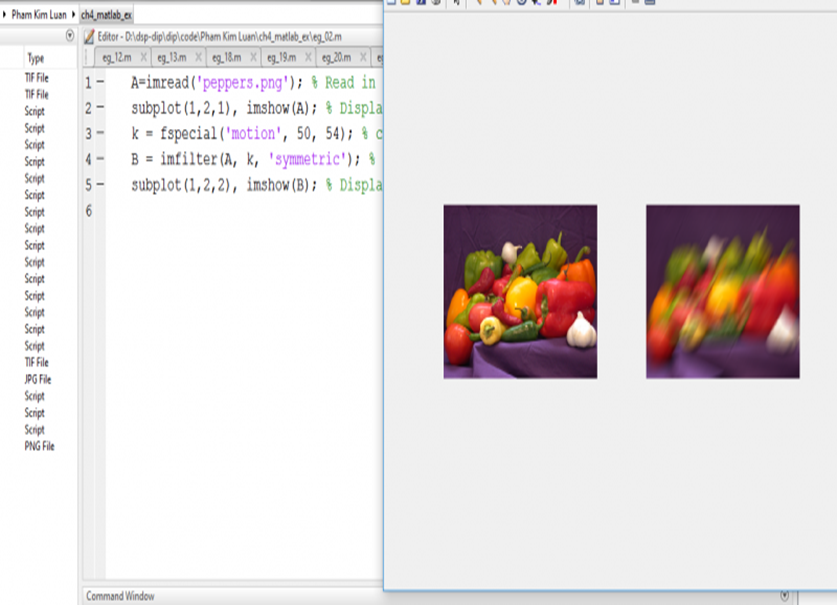
Hàm Imfilter
– Trong bộ lọc không gian tuyến tính các giá trị mới của điểm ảnh đích được xác định là sự tổ hợp tuyến tính của các giá trị điểm ảnh trong vùng lân cận. Hay nói cách khác, lọc tuyến tính là phương pháp lọc trong đó điểm ảnh của ảnh mới bằng mỗi pixel lân cận sẽ được nhân với một hệ số tương ứng rồi được cộng lại để được đáp ứng tại điểm ảnh trung tâm.
– Sự tổ hợp tuyến tính các điểm ảnh lân cận đó được xác định bởi bộ lọc kernel (thường được gọi là mặt nạ). Cơ chế của bộ lọc này là trượt kernel trên tất cả các vị trí điểm ảnh trong ảnh gốc và tính tổng các tích của điểm ảnh lân cận với hệ số bộ lọc.Kích thước bộ lọc là lẻ. Kích thước nhỏ nhất có ý nghĩa là 3×3. Hình bên dưới cho chúng ta thấy rõ được cách thực hiện của bộ lọc.
A=imread(‘peppers.png’); % Read in image
subplot(1,2,1), imshow(A); % Display image
k = fspecial(‘motion’, 50, 54); % create a 5×5 convolution kernel
B = imfilter(A, k, ‘symmetric’); % apply using symmetric mirroring at edges
subplot(1,2,2), imshow(B); % Display result image B
CHƯƠNG 4: VẼ ĐỒ THỊ HÀM SỐ Y=3×3+2×2+x+10
Mục đích của việc giải phương trình bậc 3: 3×3+2×2+x+10=0 để ta tìm điểm cực đại và cực tiểu của hàm hàm số Y=3×3+2×2+x+10 phục vụ cho việc vẽ đồ thị hàm số y=3×3+2×2+x+10 được đẹp nhất và để làm quen với giải phương trình bậc 3 bằng Matlab.
Để giải phương trình này bằng Matlab ta có nhiều cách/phương thức, ví dụ như sau:
– Cách 1: Giải phương trình bậc 3 bằng hàm roots
Bước 1: Ta xác định y1 ma trận chính là các hệ số của phương trình 3×3+2×2+x+10=0, ta có:
y1=[3 2 1 10];
Bước 2: Ta xác định nghiệm của phương trình bằng hàm roots, ta có:
>> y1=[3 2 1 10];
>> roots(y1)
ans =
-1.6667 + 0.0000i
0.5000 + 1.3229i
0.5000 – 1.3229i
– Cách 2 giải phương trình bậc 3 bằng hàm solve
Để thực hiện giải bằng hàm solve ta thực hiện các câu lệnh sau
syms(‘x’)
eqn=3*x^3+2*x^2+x+10==0
solve(eqn)
Kết quả ta có là:
eqn =
3*x^3 + 2*x^2 + x + 10 == 0
ans =
-5/3
1/2 – (7^(1/2)*1i)/2
(7^(1/2)*1i)/2 + 1/2
Vẽ đồ thị hàm số Y=3×3+2×2+x+10
Căn cứ kết quả ở trên ta xác định, đồ thị đẹp nhất là cho x chạy ngoài vùng nghiệm với x< -1.6667 + 0.0000i và x>0.5000 + 1.3229i với mật độ điểm đủ lớn để đảm bảo đồ thị được mịn. Do đó, ta cho x chạy từ -6 đến 6 với số điểm 10,000, ta có:
x=linspace(-6,6,10000);%Đặt x chạy từ -6 đến 6 với 10,000 điểm
y=3*x.^3+2*x.^2+x+10;%Đặt y =3*x^3+2*x^2+ x+10
plot(x,y,’G’)%Vẽ đồ thị hàm số y =3*x^3+2*x^2+ x+10 bằng màu xanh
xlabel(‘Trục X’)%Đặt tên cho trục X
ylabel(‘Trục Y’) %Đặt tên cho trục Y
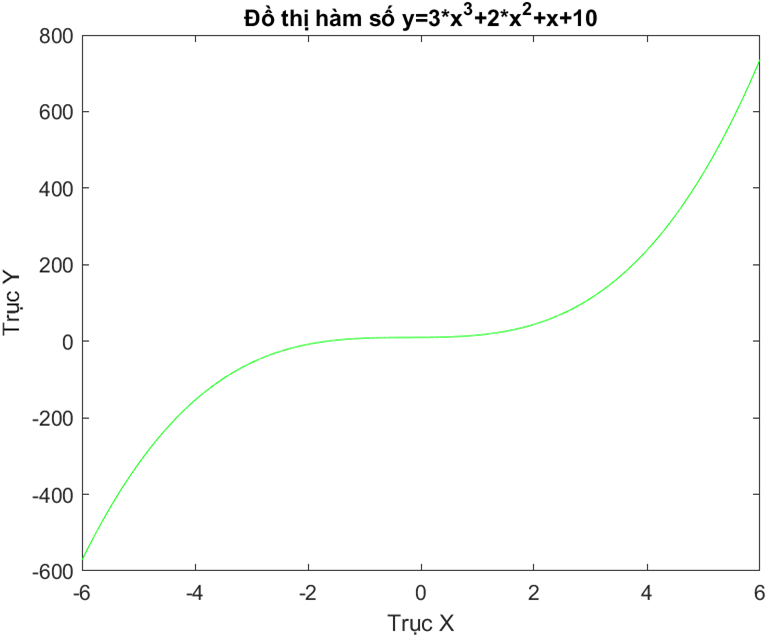
title(‘Đồ thị hàm số y=3*x^3+2*x^2+x+10’) %Đặt tiêu đề cho đồ thị hàm số
Sau khi thực thi câu lệnh trên ta có đồ thị của hàm số Y=3×3+2×2+x+10 như sau:
Đồ thị của hàm số Y=3×3+2×2+x+10
