PVWatts - ESIG - The first knowledge sharing application in Vietnam

Author: National Renewable Energy Laboratory[1]

The NREL PVWatts® calculator is a web application developed by the National Renewable Energy Laboratory (NREL) that estimates the electricity production of a grid-connected photovoltaic system based on a few simple inputs. PVWatts combines a number of sub-models to predict overall system performance, and includes several built-in parameters that are hidden from the user. This technical reference describes the sub-models, documents assumptions and hidden parameters, and explains the sequence of calculations that yield the final system performance estimate. This reference is applicable to the significantly revised version of PVWatts released by NREL in 2014.

Introduction and History

PVWatts is a popular web application for estimating the energy production of a grid-connected photovoltaic (PV) system. It is designed to be simple to use and understand for non-experts and more advanced users alike. PVWatts hides much of the complexity of accurately modeling PV systems from the user by making several hidden assumptions about the type, configuration, and operation of the system. Consequently, the results should be interpreted as being a representative estimate for a similar actual system operating in a year with typical weather. The errors may be as high as ± 10 % for annual energy totals and ± 30 % for monthly totals for weather data representing long-term historical typical conditions. Actual performance in a specific year may deviate from the long-term average up to ± 20 % for annual and ± 40 % for monthly values.

PVWatts has been online since 1999, and the original algorithms in version 1 were largely based on the approach of the Sandia PVFORM tool developed in the 1980s[2]. Since then, several versions of PVWatts have been made available, though the system performance calculations have remained largely the same as version 1.

In 2013, NREL began the process of revamping the PVWatts online web application to update the visual appeal and functionality, consolidate versions to reduce the ongoing maintenance burden, and update the energy prediction algorithms to be inline with the actual performance of modern photovoltaic systems.

While PVWatts is a useful tool for obtaining a quick estimate of energy production from a photovoltaic system, several more sophisticated tools are available for making more accurate predictions. The System Advisor Model (SAM) is a free desktop application that allows users to model PV systems in much greater detail. SAM also includes detailed economic analysis for residential, commercial, and utility-scale systems, as well as performance models for concentrating solar power (CSP), wind, solar water heating, and geothermal systems. PVsyst is another option for detailed PV performance modeling, and is a commercial software product.

Version History (current as of Feb 2014)

Version
Description
Weather Data Options
Date
Status

V1
Original online calculator
239 TMY2 sites. Added 360 international sites in 2005
1998
Retiring in 2014

V2
Modified to utilize a gridded 40 km monthly weather data in the continental US. Hourly calculations were done with the nearest TMY2 site, and then the monthly totals were scaled using the monthly gridded weather data.
CSR 40-km gridded monthly irradiance & temperature
2001
Retiring in 2014

SOAP
A web service version of V2 using the SOAP protocol for monthly predictions
Same as V2
2003
Retiring in 2014

V3
Web service version of the hourly PVWatts V1 using the 10-km hourly satellite-based irradiance dataset. Included a simplified economic cash flow calculation
NREL/Clean Power Research Perez 10-km satellite-based irradiance, typical files created from 1998-2005 period of record
2009
Defunct in 2012

V4
Updated REST-ful web service of the hourly PVWatts V1 on http://developer.nrel.gov
239 TMY2s, 1020 TMY3s, 360 International, 10 km CPR/Perez 1998-2009 typical satellite
2012
Operational

V5
Completely new web application user interface, updated calculation engine (described here). Available at http://pvwatts.nrel.gov. Also available as a web service on http://developer.nrel.gov
1020 Class I and II TMY3s (default), 239 TMY2s, 360 International, 10 km CPR/Perez 1998-2009 typical satellite
2012
Forthcoming in 2014

Overview of Changes in Newest Version (Version 5)

PVWatts Version 5 is a comprehensive update of both default values and calculation methods. The changes are designed to more accurately model typical systems while keeping the number of inputs to a minimum, and to provide a way to differentiate between common technology options without posing undue technical burdens upon the user.

For reference, previous versions of the PVWatts calculations are described in [2]. The key changes in PVWatts V5 are:

Option to select “Standard”, “Premium”, or “Thin film” module type
The option to specify a DC-to-AC nameplate sizing ratio
Module model no longer includes a quadratic correction at low light levels
Total system losses are specified as a percentage, with a default value of 14 %. This replaces the former DC-to-AC derate factor in PVWatts V1.
Inverter efficiency curve is derived from statistical analysis of data on inverters manufactured since 2010. The nominal inverter efficiency can be entered by the user.
One-axis tracking systems either estimate linear beam+diffuse self-shading losses based on row spacing, or use backtracking.
Albedo is fixed at 0.2 unless explicitly specified at each hour in a TMY3, EPW, or SAM/CSV weather file

Model Inputs

PVWatts requires the minimal set of PV system specifications. Other performance parameters such as module temperature coefficients are hidden from the user.

Input Parameter

Field
Units
Default Value

System size
kW (DC)
4

Module type
Standard, Premium, Thin film
Standard

System losses
%
14

Array type
Fixed open rack, Fixed roof mount, 1-Axis, Backtracked 1-Axis, 2-Axis
Fixed open rack

Tilt angle
degrees
Site Latitude

Azimuth angle
degrees
180° in northern hemisphere, 0° in southern hemisphere

Advanced inputs

DC/AC ratio
ratio
1.1

Inverter efficiency
%
96

GCR (1 Axis only)
fraction
0.4

The new module type input is designed to help differentiate between different technology options. The “standard” option is intended to represent typical poly- or mono-crystalline silicon modules, with efficiencies in the range of 14-17 %. The “premium” option is appropriate for modeling high efficiency (~18-20 %) monocrystalline silicon modules that have anti-reective coatings and lower temperature coefficients. The thin film option assumes a low efficiency (~11 %), and a significantly lower temperature coefficient which is representative of most installed thin film modules as of 2013. It is important to note that less common thin film module technologies may have quite different temperature coefficients than the default. It is up to the user to select the most appropriate option for the type of module being considered based on information on the module data sheet. The “standard” option is appropriate for typical preliminary analyses and is most similar to PVWatts V1.

Assumptions for different module types

Module type
Efficiency
Cover type
Temperature coefficient

Standard
~15 %
Glass
-0.47 %/°C

Premium
~19 %
Anti-reflective
-0.35 %/°C

Thin film
~10 %
Glass
-0.20 %/°C

The new advanced inputs allow the user to specify a DC-to-AC sizing ratio and ground coverage ratio, which was not possible in older versions of PVWatts. PVWatts V1 assumed that the DC nameplate capacity of the system was equal to the AC nameplate capacity. In modern systems, the photovoltaic array is often sized so that its DC rating is higher than the inverter’s AC rating. Depending on location, this may be desirable to capture more energy during the beginning and end of the day, despite possibly clipping output at peak sun hours. The default value of the new DC-to-AC ratio input is 1.1. For a 4 kW DC system with the default value, the inverter would be 3.63 kW AC.

The ground coverage ratio (GCR) only applies to one axis tracking systems, and is a measure of the total module area relative to the roof or ground space they occupy. A GCR of 0.5 means that for a horizontal roof or ground surface, half of the total area is covered by modules when the tracker is rotated such that they are horizontal. A lower GCR means wider spacing between rows, and a larger one means that rows are spaced closer together. A GCR of 1 indicates no space between adjacent rows, and a GCR of 0 means essentially infinite spacing between rows. Typical one axis tracker systems have GCRs in the range of 0.3 to 0.6, and the default value in PVWatts is 0.4. Previous versions of PVWatts essentially assumed a GCR of zero, which is impossible to achieve in practice.

Solar Resource

The PVWatts model is an hourly simulation program that requires hourly data for one year for two components of solar irradiance (beam and diffuse), as well as ambient dry bulb temperature and wind speed at 10 m above the ground. PVWatts requires that each hour be timestamped with the year, month, day, and hour corresponding to the data line so that the sun position can be accurately calculated.

No adjustments are made for leap years or daylight savings time: hence, “hourly data” in this context implies 8,760 data points for one year.

Header Information

Field
Units

Latitude
degrees

Longitude
degrees

Time zone
hours offset from Greenwich Mean Time

Site elevation
meters above sea level

PVWatts can read solar resource data files from different sources and in different formats, including the National Solar Radiation Database (NSRDB) 1961-1990 data (http://rredc.nrel.gov/solar/old_data/nsrdb/1961-1990/tmy2/ TMY2]) and 1991-2010 update (TMY3), and EnergyPlus weather files. It also reads files in the SAM CSV format, which is a generic format suitable for custom solar resource data sets. The PVWatts web application interacts with three online databases to access solar resource data, but does not allow users to specify their own weather data.

Hourly Input Data Fields

Field
Units/Values

Year
1950-2050

Month
1-12

Day
1-31

Hour
0-23

Direct normal irradiance (DNI)
W/m2

Diffuse horizontal irradiance (DHI)
W/m2

Ambient dry bulb temperature
Celsius

Wind speed at 10 m
m/s

Albedo (optional, typically in TMY3 files)
[0..1]

Sun Position

At each hour, PVWatts calculates the sun position using the algorithm described in Astronomical Almanac[3]. The sun position is calculated at the midpoint of the hour: for example, from 2 p.m. to 3 p.m., the sun position is calculated at 2:30 p.m. to determine the solar zenith and azimuth angles. This is the case for normal daytime hours during which the sun is above the horizon for the whole hour.

For the sunrise hour, the midpoint between the sunrise time and the end of the timestep is used for the sun position calculation. Analogously, the midpoint between the beginning of the timestep and sunset time is used for the sunset hour.

Tracking

PVWatts performs angle of incidence (AOI) (α) calculations for fixed, one-axis, or two-axis tracking systems.

Fixed systems implement standard geometrical calculations for the angle of incidence given surface tilt β, surface azimuth γ, solar azimuth γsun, and solar zenith θsun angles

\(\alpha_{fixed}-cos^{-1}\left (sin(\theta_{sun})cos(\gamma\text{ }\text{ }\text{ } \gamma_{sun})sin(\beta)+cos(\theta_{sun})cos(\beta)\right )\)

For one axis trackers, the algorithm documented in Rotation Angle for the Optimum Tracking of One-Axis Trackers is used. It assumes ideal tracking and does not account for any shading. The one-axis tracking algorithm assumes a hard-coded rotation limit of ± 45 degrees from the horizontal. PVWatts uses a separate algorithm to calculate the fraction of each row that is shaded by adjacent rows, and reduces the beam and diffuse irradiance incident on each row accordingly. This simplified approach does not require information about row dimensions. When the backtracking option is enabled, PVWatts uses the SAM backtracking algorithm to avoid self-shading of adjacent rows. For details on these algorithms, consult SAM Photovoltaic Model Technical Reference.
For two axis tracking systems, the PV surface tilt and azimuth are set equal to the sun zenith angle and the sun azimuth angle, respectively, and the incidence angle is zero.

Plane-of-Array Irradiance

The plane-of-array (POA) beam, sky diffuse, and ground-reflected diffuse irradiance components are calculated using the Perez 1990 algorithm[4]. The POA beam component Ib is simply the beam normal input multiplied by the cosine of the angle of incidence. The isotropic, circumsolar, and horizon brightening diffuse terms are calculated from the beam and diffuse input given two empirical functions F1 and F2 as defined and are summed to yield the total sky diffuse on the surface Id,sky. A slight modification from the standard Perez model treats the diffuse irradiance as isotropic for zenith angles between 87.5 and 90 degrees. The ground reflected irradiance Id,ground is treated as isotropic diffuse with a view factor calculated from the ground with respect to the tilted surface. The total POAincident on the module cover is the sum of the three components

\(I_{poa}-I_b+I_{d,sky}+I_{d,ground}\)

The albedo, or ground reflectance, is by default fixed at 0.2. When using TMY3 data as input, and valid data is found in the albedo column, the reported albedo from the data file is used.

Module Cover

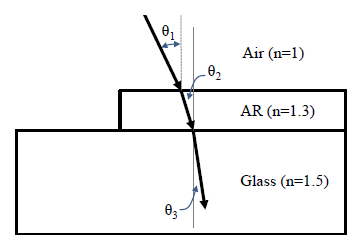
Given the total POA irradiance incident on the module cover, PVWatts applies an AOI correction to adjust the direct beam irradiance to account for reflection losses. The correction uses a modified version of the physical model of transmittance through a module cover used in [5].

PVWatts V5 gives users the option of “Standard”, “Premium”, or “Thin film” modules. For standard and thin film modules, PVWatts uses a single slab, calculating the transmittance through glass with index of refraction of 1.526. This follows the treatment in [5], with the simplification of removing the absorptance term which is determined (see below) to have a negligible effect.

For the premium module option, a two slab approach is used to model both the glass and the thin anti-reflective (AR) coating that is designed to improve the angular response. The two slab model involves predicting the transmittance of irradiance through two materials. The model applies the physical representation for unpolarized radiation described in [5] twice: once for the anti-reflective (AR) coating, and subsequently for the glass cover.

First, the angle of refraction θ2 into the AR coating is calculated with Snell’s law given angle of incidence θ1

\(\theta_2-arcsin\left (\cfrac{n_{air}}{n_{AR}}sin(\theta_1)\right )\)

Next, the transmittance through the AR coating is calculated from Fresnel’s equation for non-reflected unpolarized radiation, which takes the average of parallel and perpendicular components:

\(\tau_{AR}-1\text{ }\text{ }\text{ } 0.5\left (\cfrac{sin(\theta_2\text{ }\text{ }\text{ } \theta_1)^2}{sin(\theta_2+\theta_1)^2}+\cfrac{tan(\theta_2\text{ }\text{ }\text{ } \theta_1)^2}{tan(\theta_2+\theta_1)^2}\right )\)

The angle of refraction into the glass cover θ3 is again determined from Snell’s law:

\(\theta_3-arcsin\left (\cfrac{n_{AR}}{n_{glass}}sin(\theta_2)\right )\)

The transmittance through the glass is calculated similarly given θ2 and θ3:

\(\tau_{glass}-1\text{ }\text{ }\text{ } 0.5\left (\cfrac{sin(\theta_3\text{ }\text{ }\text{ } \theta_2)^2}{sin(\theta_3+\theta_2)^2}+\cfrac{tan(\theta_3\text{ }\text{ }\text{ } \theta_2)^2}{tan(\theta_3+\theta_2)^2}\right )\)

Finally, the effective transmittance through the AR coated module cover is given by:

\(\tau_{cover}-\tau_{AR}\tau_{glass}\)

Desoto suggests using Bouguer’s law to estimate the absorption, but for typical dimensions (~2 mm) and extinction coefficients (K ≈ 4) in this application, the absorption is predicted to be less than 0.1 % and is thus ignored.

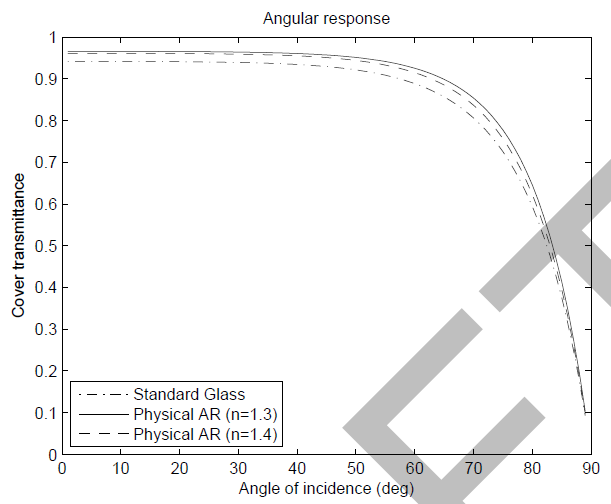
Given nair = 1 and nglass = 1.526. The model suggests that an AR coating yields an improvement in transmittance of about 3 % relative to standard glass at normal incidence, which is commensurate with claims made by industry (Honeywell SOLARC, DSM Khepricoat).

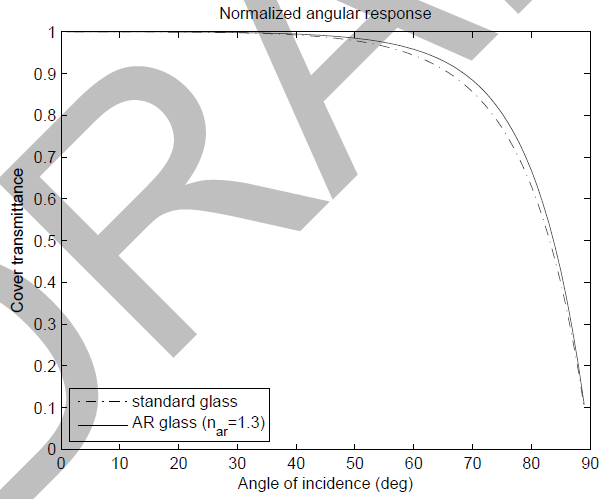
Normalizing the response curve to normal incidence shows that the model predicts an improvement in light capture at high incidence angles for AR glass, which agrees with data from manufacturers of AR coated modules (Normalized angular response figure).

For the standard glass model, the difference in power output is negligible, and the AR glass option will predict slightly higher output due to the improved angular response. The higher normal incidence reflectivity of the module is assumed to be captured in the nameplate rating of the system. The additional energy output due to the better angular response is slight: for a fixed south-facing system in Texas, the anti-reflective coating yielded about ~0.5 % more energy on an annual basis. This will vary depending on location and system parameters.

Thermal Model

PVWatts implements a thermal model to calculate the operating cell temperature Tcell using a first-principles heat transfer energy balance model developed by Fuentes. The Fuentes model includes effects of the thermal capacitance of the module and performs a numerical integration between timesteps to account for the thermal lag transient behavior. The thermal model uses the total incident POA irradiance, wind speed, and dry bulb temperature to calculate the operating cell temperature. PVWatts assumes that the system is installed at a height of 5 m, and that the installed nominal operating cell temperature (INOCT) of the module is 45°C.

The Fuentes paper discusses translation of the nominal operating cell temperature (NOCT) measured at standard conditions (800 W/m2, 20°C ambient) to INOCT based on mounting configuration. For a roof mount system, air flow around the modules more restricted than on an open rack, and the installed nominal operating temperature will be higher. The estimate is for INOCT to be roughly 49°C for 4 inch standoffs. For fixed open rack and tracking systems, the original PVWatts V1 assumption of 45°C INOCT is retained.

Module Model

The PVWatts module computes the DC power from the array with a specified nameplate DC rating of Pdc0 given a computed cell temperature Tcell and transmitted POA irradiance Itr. The array efficiency is assumed to decrease at a linear rate as a function of temperature rise, governed by temperature coefficient γ. The reference cell temperature Tref is 25°C, and reference irradiance is 1000 W/m2

\(P_{dc}-\cfrac{I_{tr}}{1000}P_{dc0}\left (1+\gamma(T_{cell}\text{ }\text{ }\text{ } T_{ref})\right )\)

The temperature coefficient is changed depending on the module type selected. The values used are determined from a statistical analysis of over 11000 modules in the CEC module database.

System Losses

Losses in the system that are not explicitly modeled are provided by the user as a percentage. Losses represented by this number include the impacts of soiling, shading, snow cover, mismatch, wiring, connections, light induced degradation, nameplate rating, system age, and operational availability.

System Losses

Loss mechanism
Default value

Soiling
2 %

Shading
3 %

Snow
0 %

Mismatch
2 %

Wiring
2 %

Connections
0.5 %

Light-induced degradation
1.5%

Nameplate rating
1 %

Age
0 %

Availability
3 %

Total losses
14 %

It is important to note that the total loss is not the sum of the individual losses. The total loss is calculated by multiplying the reduction due to each loss Li (%). The default total system loss is calculated to be 14 %

\(L_{total}(\%)-100\left [1\text{ }\text{ }\text{ } \prod_{i} \left (1\text{ }\text{ }\text{ } \cfrac{L_i}{100}\right )\right ]\)

Light-induced degradation (LID) is a phenomenon in which the power output of a module decreases when it is exposed to sunlight for the first time. After this initial period, the module power stabilizes and subsequently follows typical long-term degradation over the lifetime of the installation (~0.5 %/year). The default light-induced degradation (LID) loss of 1.5 % is a typical value based on measurements of losses in different module types ??. Some premium modules may experience lower LID losses due to their materials and construction, while others may experience LID losses much greater than 1.5 %.

To approximately convert PVWatts V5 system loss to a PVWatts V1 DC-to-AC derate factor:

Convert the system loss to a derate: 1 – 14=100 = 0.86.
Multiply this value by the nominal inverter efficiency: 0.86 x 0.96 = 0.825

This suggests that the default PVWatts V5 system loss represents roughly a 7 % increase in system performance relative to PVWatts V1 due solely to updated input assumptions. The impact of the revised inverter efficiency curve in version 5 (described in next section) places the realized performance gain relative to V1 closer to 8-9 % on an annual energy basis. This behavior is commensurate with hundreds of reports from PVWatts users, and expert survey solicitation, and calibration to numerous measured datasets that suggested that the old PVWatts derate was too conservative and underpredicted modern system performance by at least 8-9 % on average.

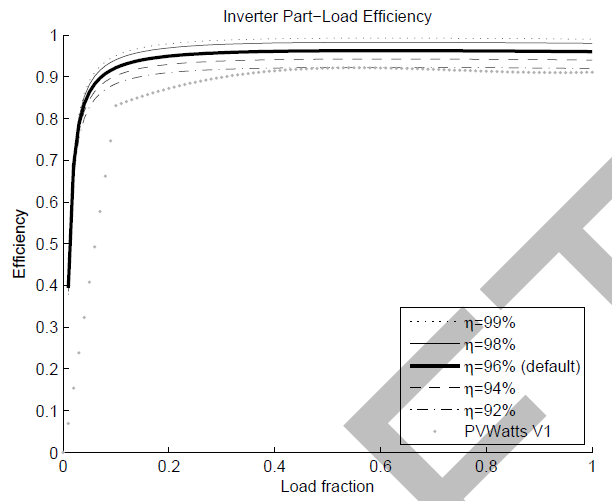
Inverter Model

The inverter model in PVWatts V5 is based on an analysis of California Energy Commission (CEC) inverter performance data. Inverters newer than 2010 were included in the analysis. A “typical” inverter was selected from the dataset by first calculating an average part-load efficiency curve, and then finding the actual inverter in the dataset whose actual efficiency curve was closest to the average. The efficiency data was then fitted to a quadratic loss model as presented in[6]. The resulting performance curve is given in following equation, which scales the efficiency curve to the nominal rated efficiency specified by the user nnom. The nominal inverter efficiency from the CEC data for the actual most typical inverter is nref is 0.9637 (Pac0/Pdc0), and AC nameplate rating Pac0 is determined from the DC rating of the system and the DC-to-AC ratio. The default nominal efficiency nnom is 0.96

\(\eta-\cfrac{\eta_{nom}}{\eta_{ref}}\left (0.0109\cdot \zeta\text{ }\text{ }\text{ }\text{ }\text{ }\text{ } \cfrac{0.0051}{\zeta}+0.9888\right )\text{ }\text{ }\text{ }\)

where \(\text{ }\text{ }\text{ }\zeta-\cfrac{P_{dc}}{P_{dc0}}\text{ }\text{ }\text{ }\) and \(\text{ }\text{ }\text{ }P_{dc0}-\cfrac{P_{ac0}}{\eta_0}\)

When the predicted AC output exceeds the nameplate rating, the output is clipped to the nameplate value. The inverter efficiency is shown the for different nominal efficiencies, along with the original version 1 curve:

\(P_{ac} –
\begin{cases}
\eta P_{dc} & :0<P_{dc}<P_{dc0} \\
P_{ac0} & :P_{dc}\ge P_{dc0} \\
0 & :P_{dc}-0
\end{cases}\)

Model Outputs

\(P_{ac} –\begin{cases}\eta P_{dc} & :0

PVWatts calculates several hourly outputs based on the system specifications and hourly irradiance, temperature, and wind speed data.

In addition, the average incident POA irradiance per day in each month is reported to the user. For each month m, the average POA in (kW/m2/day) is given by

\(POA_m-\cfrac{0.001\cdot \sum_{m} POA_h}{\text{number of days in month } m}\)

The hourly outputs DC and AC power are also aggregated into monthly and annual energy totals that are reported to the user.

Hourly Calculated Outputs

Field
Units

Incident POA irradiance
W/m2

Transmitted POA irradiance
W/m2

DC power
W

AC power
W

Comparison with Measured Data

In this section, PVWatts predictions are shown for several systems. The nine systems considered are detailed in[7], and consist of 8 fixed tilt systems and one 1-axis tracked system. PVWatts V1 underpredicts system performance by appoximately 14 % when comparing annual AC energy. However, these systems were unshaded, and the periods during which the system was unavailable were removed from the comparison. Removing these loss mechanisms, the effective PVWatts V5 derate would be about 0.877, which is about 13.8 % higher than the default PVWatts V1 derate of 0.77 and would roughly compensate for the ~14 % underprediction indicated in the PVWatts V1 validation.

In the Hourly AC Production-Modeled vs Measured figure, PVWatts V1 hourly results are shown for a fixed crystalline silicon system in Colorado. The data suggests a quadratic behavior at low power levels, which is corrected in PVWatts V5 by removing the performance adjustment below 125 W/m2. The PVWatts V1 low irradiance assumptions are not supported by any of the modern systems considered.

Conclusions

A comprehensive update to the popular PVWatts photovoltaic performance model was presented. The improved model formulation and updated default assumptions largely correct the often reported underprediction of previous model versions (V1) relative to actual system performance.

The updated calculation engine will be deployed to the NREL PVWatts Online Calculator in the second half of 2014, available at http://pvwatts.nrel.gov.

References

↑
NREL, PVWatts Version 5 Manual, March 2014, [Online]. Available: https://sam.nrel.gov/sites/sam.nrel.gov/files/content/documents/pdf/pvwattsv5-draft-march-14-2014.pdf [Accessed May 2014].
2.0 2.1
Dobos, A.; PVWatts Version 1 Technical Reference. . NREL/TP-6A20-60272. 2013.
↑
Michalsky, J. (1988). \The Astronomical Almanac’s Algorithm for Approximate Solar Position (1950-2050).” Solar Energy (40).
↑
Perez, R.; Ineichen, P.; Seals, R.; Michalsky, J.; Stewart, R. (1990). \Modeling Daylight Availability and Irradiance Components for Direct and Global Irradiance.” Solar Energy (44:5), pp. 271-289.
5.0 5.1 5.2
DeSoto, W.; Klein, S.; Beckman, W.; Improvement and Validation of a Model for Photovoltaic Array Performance. Solar Energy, vol.80, pp.78-88, 2006.
↑
Dreisse, A.; Jain, P.; Harrison, S.; Beyond the Curves: Modeling the Electrical Efficiency of Photovoltaic Inverters. Proc. IEEE Photovoltaic Specialists Conf., 2008.
↑
Freeman, J.; Whitmore, J.; Kaffine, L.; Blair, N.; Dobos, A.; System Advisor Model: Flat Plat Photovolatic Performance Modeling Validation Report. NREL/TP-6A20-60204, 2013.

PVWatts – ESIG