ỨNG DỤNG TÍNH CHẤT TAM GIÁC ĐỒNG DẠNG ĐỂ GIẢI QUYẾT CÁC BÀI TOÁN THỰC TẾ – BITEXEDU
Toán thực tế là một chủ đề rất hay, thường được đưa vào các đề thi nhằm tăng khả năng vận dụng các kiến thức vào thực tiễn của học sinh. Ngoài ra, tam giác đồng dạng có khá nhiều ứng dụng trong thực tế, đặc biệt là trong đo đạc. Dưới đây là một số bài toán thực tế đã xuất hiện trong các đề thi học kỳ 2 lớp 8 ở một số Quận ở TPHCM và được giải quyết bằng cách vận dụng tính chất tam giác đồng dạng.
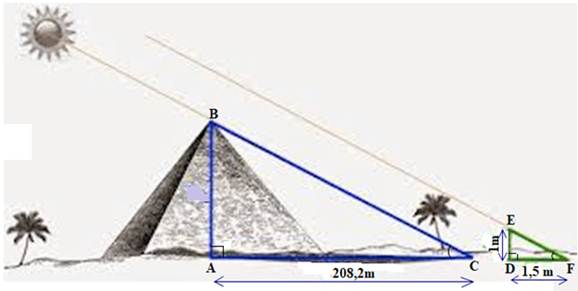
Bài toán 1. (đề thi Quận 10- 2017/2018) Kim tự tháp là niềm tự hào của người dân Ai Cập. Để tính được chiều cao gần đúng của Kim tự tháp, người ta làm như sau: đầu tiên cắm 1 cây cọc cao $latex 1\left( m \right)$ vuông góc với mặt đất và đo được bóng cọc trên mặt đất là $latex 1,5\left( m \right)$ và khi đó chiều dài bóng Kim tự tháp trên mặt đất là $latex 208,2\left( m \right)$. Hỏi Kim tự tháp cao bao nhiêu mét ? (xem hình vẽ)
Hướng dẫn giải
Xét vuông tại A và $latex \Delta DEF$ vuông tại D ta có $latex \hat{C}=\hat{F}$
Suy ra: $latex \Delta ABC\sim \Delta DEF$ $latex \Rightarrow \dfrac{AC}{DF}=\dfrac{AB}{DE}$ $latex \Rightarrow AB=\dfrac{AC\times DE}{DF}$ $latex =\dfrac{208.2}{1.5}=138.8(m)$
Vậy Kim Tử Tháp cao $latex 138.8\left( m \right)$
Bài toán 2. Một người đo chiều cao của một cây cao nhờ một cột chôn xuống đất cọc cao $latex 2\left( m \right)$ và được đặt cách xa cây $latex 15\left( m \right)$. Sau đó, người này lùi ra xa cọc $latex 0.8\left( m \right)$ thì nhìn thấy đầu cọc và ngọn cây nằm trên một đường thẳng. Tính chiều cao cây, biết rằng khoảng cách từ chân tới mắt người đó là $latex 1.6\left( m \right)$.
- $latex 10.6\left( m \right)$
- $latex 9.5\left( m \right)$
- $latex 9.1\left( m \right)$
- $latex 10.7\left( m \right)$
Hướng dẫn giải.
Từ dữ liệu đề bài, chúng ta mô phỏng lại bằng hình vẽ sau
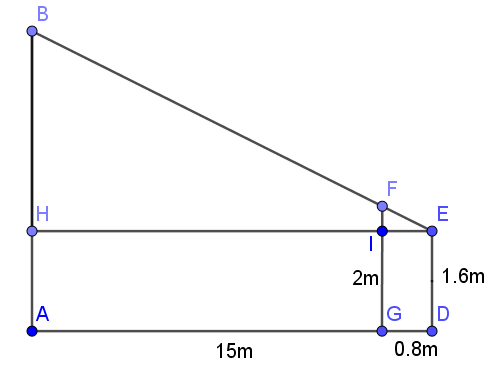
Trong đó $latex AB$ là cây cần đo chiều cao, $latex FG$ là cọc và $latex ED$ là khoảng cách từ chân tới mắt người đo
Như vậy, theo đề bài ta có: $latex AG=15\left( m \right)$, $latex GD=0.8\left( m \right)$, $latex ED=1.6\left( m \right)$, $latex GF=2\left( m \right)$
Ta có: $latex FI\parallel BH$ suy ra $\Delta EIF\sim \Delta EHB\\$
$latex \Rightarrow \dfrac{IF}{HB}=\dfrac{EI}{EH}$ $latex \Rightarrow HB=\dfrac{EH\times IF}{EI}$ $latex =\dfrac{\left( 15+0.8 \right)\times \left( 2-1.6 \right)}{0.8}$$=7.9\left( m \right)\\$
$ AB=AH+HB=1.6+7.9=9.5\left( m \right)\\$
Đáp án B
Bài toán 3.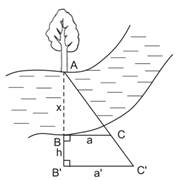 Người ta có thể đo đạc các yếu tố hình học cần thiết để tính chiều rộng của khúc sông mà không cần phải sang bờ bên kia. Nhìn hình bên cạnh, hãy tính khoảng cách $latex AB = x$ biết $latex a = 5\left( m \right)$, $latex a’ = 7\left( m \right)$ và $latex h = 2\left( m \right)$.
Người ta có thể đo đạc các yếu tố hình học cần thiết để tính chiều rộng của khúc sông mà không cần phải sang bờ bên kia. Nhìn hình bên cạnh, hãy tính khoảng cách $latex AB = x$ biết $latex a = 5\left( m \right)$, $latex a’ = 7\left( m \right)$ và $latex h = 2\left( m \right)$.
Hướng dẫn giải
Ta có $latex BC\bot A{B}’$ và $latex {B}'{C}’\bot A{B}’$ suy ra $latex BC\parallel {B}’C$
Như vậy $latex \Delta ABC\sim \Delta A{B}'{C}’$ (g-g)
Theo tính chất tam giác đồng dạng ta có: $latex \dfrac{AB}{A{B}’}=\dfrac{BC}{{B}'{C}’}$ $latex \Rightarrow \dfrac{x}{x+h}=\dfrac{a}{{{a}’}}$ hay $latex \dfrac{x}{x+2}=\dfrac{5}{7}$
Khai triển phương trình trên ta có $latex 2x=10$ $latex \Rightarrow x=5$
Vậy khoảng cách hai bờ bằng $latex 5\left( m \right)$
Cảm ơn các bạn đã theo dõi bài viết ỨNG DỤNG TÍNH CHẤT TAM GIÁC ĐỒNG DẠNG ĐỂ GIẢI QUYẾT CÁC BÀI TOÁN THỰC TẾ. Mọi ý kiến đóng góp và các câu hỏi thắc mắc về bài viết cũng như các vấn đề về máy tính Casio fx 580vnx , bạn đọc có thể gởi tin nhắn trực tiếp về fanpage DIỄN ĐÀN TOÁN CASIO
Chia sẻ
Mục lục bài viết
About Ngọc Hiền Bitex
![]()











