Bài tập hệ thức Viet – Có đáp án và PDF luyện tập – Học Tốt Blog
Trong các bài viết trước, chúng ta đã được tìm hiểu về Hệ thức Vi-et và Các dạng bài hệ thức Viet. Trong bài viết này, HOCMAI đã tổng hợp một số
Bài tập hệ thức Viet
với
cấp độ từ cơ bản đến nâng cao giúp các bạn nắm vững kiến thức, nhận biết và ứng dụng được hệ thức này.
Xem lại bài viết trước:
Mục lục bài viết
Bài tập hệ thức Viet kèm lời giải chi tiết
Bài 1: Cho phương trình: x2 + (2m -1)x – m = 0.
a) Chứng minh: P.trình luôn có nghiệm với mọi m.
b) Gọi 2 nghiệm của phương trình trên là x1, x2. Tìm g.trị của m để biểu thức A= x1^2 + x2^2 – x1.x2 có GTNN.
Lời giải
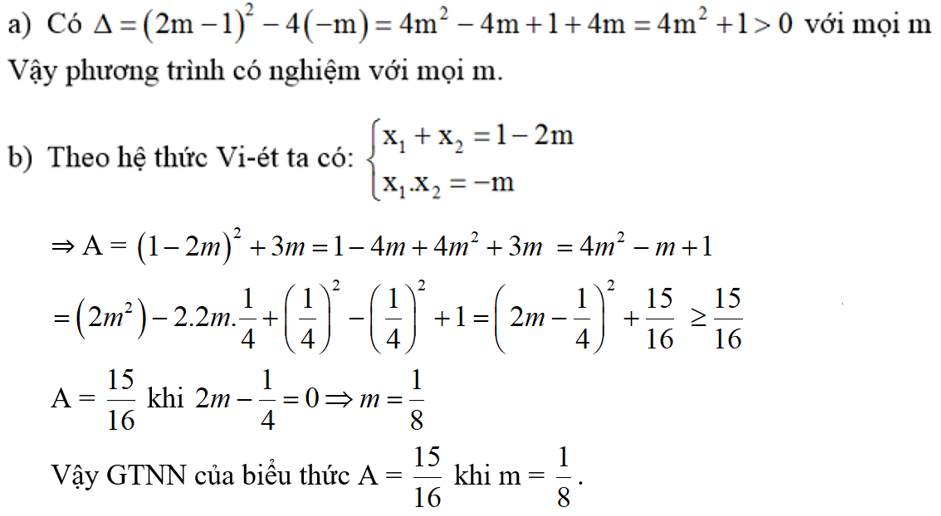
Bài 2: Cho phương trình x^2 + 2x + k = 0.
Tìm k để p.trình có hai nghiệm x1 và x2 thỏa mãn một trong bốn điều kiện sau:
a) x1 – x2 = 14
b) x1 = 2x^2
c) x1^2 + x2^2 = 1
d) 1/x1 + 1/x2 = 2
Lời giải


Bài 3: Cho phương trình bậc hai x^2 – 2(m+1)x + m – 4 = 0
a) Chứng minh: Với mọi m, P.trình luôn có 2 nghiệm phân biệt.
b) P.trình luôn có hai nghiệm trái dấu khi m có giá trị bằng?
c) Tìm một biểu thức liên hệ giữa hai nghiệm không phụ thuộc vào m mà không cần giải phương trình.
Lời giải
a) P.trình có 2 nghiệm phân biệt với mọi g.trị m ⇔ Δ > 0 với mọi m
Ta có Δ’ = (m +1)^2 – (m – 4) = m^2 + m + 5 = (m + 1/2)^2 + 19/4 > 0 với mọi m
=> Phương trình luôn có 2 nghiệm phân biệt.
b) P. trình sẽ có hai nghiệm trái dấu khi và chỉ khi:
ac < 0 ⇔ m – 4 < 0 ⇔ m < 4
Vậy khi m < 4 thì p.trình có 2 nghiệm trái dấu.

Bài 4: Phương trình x^2 + (√3 + 1)x + √3
Có hai nghiệm phân biệt là x1 và x2. G.trị của biểu thức x1^2.x2 + x1.x2^2 bằng:
-
-3 – √
3
- √3
–
3
- √3
+
3
-
3
– √3
Lời giải

Vậy A là đáp án chính xác
Bài 5: Cho phương trình x^2 – 2x – 3 = 0
Gọi tổng và tích hai nghiệm của phương trình trên là là S và P. Tìm S2 + 2P?
Lời giải

Bài 6: Cho p.trình x2 – (m2 + 1)x + 3m2 – 8 = 0 ( tham số m).
Tìm các giá trị của m để p.trình có hai nghiệm phân biệt là x1, x2. Lưu ý: Cần thỏa mãn điều kiện: x1 = 4×2 là:
Lời giải
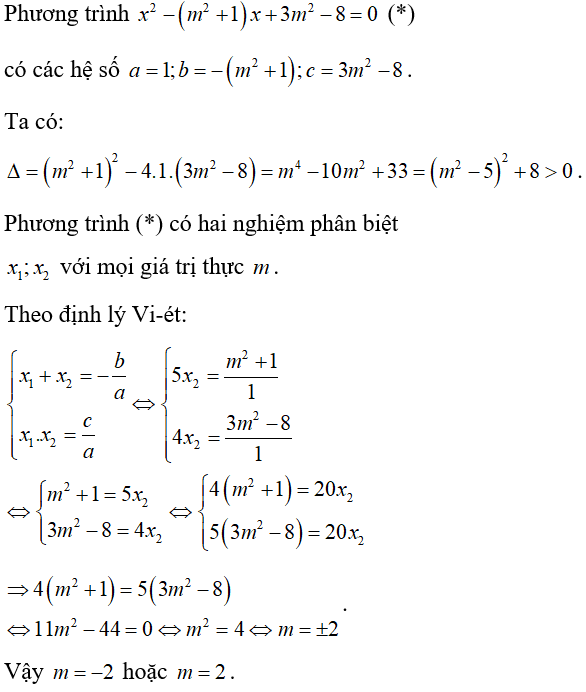
Bài 7: Cho phương trình x2 + mx – 2 = 0
Trong các phương trình sau, phương trình nào có nghiệm bằng nghịch đảo các nghiệm của phương trình trên?
a) -2x^2 + mx – 2 = 0
b) x^2 – mx – 1 = 0
c) x^2 + mx – 1 = 0
d) 2x^2 – mx – 2 = 0
Lời giải

Vậy D là đáp án chính xác
Bài 8: Cho p.trình x^2 – 2x – m2 = 0 có hai nghiệm x1, x2.
P.trình bậc hai một ẩn có hai nghiệm là y1 = 2×1 – 1 và y2 = 2x^2 – 1 là:
Lời giải

Bài 9: Cho p.trình bậc hai ẩn x, tham số m: mx^2 – (2m + 3)x + m – 4 = 0.
Với các g.trị của m để p.trình có hai nghiệm x1, x2. Tìm biểu thức liên hệ giữa hai nghiệm không phụ thuộc vào m.
a) 3(x1 + x2) + 4x1x2 = 11
b) 4(x1 + x2) + 3x1x2 = 11
c) 3(x1 + x2) + 4x1x2 = 1
d) 3(x1 + x2) – 4x1x2 = 11
Lời giải

Vậy B là đáp án chính xác
Bài 10: Cho phương trình: x^2 – (2m + 3)x + m = 0
a. Hãy chúng minh phương trình có nghiệm với mọi m
b. Gọi x1, x2 là nghiệm của ph.trình, tìm m để x1^2 + x2^2 có GTNN
Lời giải

Bài tập thêm để luyện tập:
Tham khảo thêm:
Bài viết trên là một số Bài tập hệ thức Viet và lời giải chi tiết. Nếu có câu hỏi về nội dung bài viết hoặc chủ đề cần giải đáp, hãy để lại phần bình dưới bài viết này nhé! Hẹn gặp lại các bạn ở bài viết tiếp theo của HOCMAI nhé!











