Lịch sử toán học – Wikipedia tiếng Việt

Từ toán học có nghĩa là “khoa học, tri thức hoặc học tập”. Ngày nay, thuật ngữ “toán học” chỉ một bộ phận cụ thể của tri thức – ngành nghiên cứu suy luận về lượng, cấu trúc, và sự thay đổi; là ngôn ngữ của vũ trụ.[1] Lĩnh vực của ngành học về Lịch sử Toán học phần lớn là sự nghiên cứu nguồn gốc của những khám phá mới trong toán học, theo nghĩa hẹp hơn là nghiên cứu các phương pháp và ký hiệu toán học chuẩn trong quá khứ.

Trước thời kì hiện đại và sự phổ biến rộng rãi tri thức trên toàn thế giới, các ví dụ trên văn bản của các phát triển mới của toán học chỉ tỏa sáng ở những vùng, miền cụ thể. Các văn bản toán học cổ nhất từ Lưỡng Hà cổ đại (Mesopotamia) khoảng 1900 TCN (Plimpton 322), Ai Cập cổ đại khoảng 1800 TCN (Rhind Mathematical Papyrus), Vương quốc Giữa Ai Cập khoảng 1300-1200 TCN (Berlin 6619) và Ấn Độ cổ đại khoảng 800 TCN (Shulba Sutras). Tất cả các văn tự này có nhắc đến Định lý Pythagore; đây có lẽ là phát triển toán học rộng nhất và cổ nhất sau số học cổ đại và hình học.

Những góp sức của Hy Lạp cổ đại với toán học, nhìn chung được coi là một trong những góp sức quan trọng nhất, đã tăng trưởng tỏa nắng rực rỡ cả về chiêu thức và vật liệu chủ đề của toán học. [ 2 ]

Một đặc điểm đáng chú ý của lịch sử toán học cổ và trung đại là theo sau sự bùng nổ của các phát triển toán học thường là sự ngưng trệ hàng thế kỉ. Bắt đầu vào Thời kì Phục Hưng tại Ý vào thế kỉ 16, các phát triển toán học mới, tương tác với các phát hiện khoa học mới, đã được thực hiện với tốc độ ngày càng tăng, và điều này còn tiếp diễn cho tới hiện tại.

Toán học thời sơ khai[sửa|sửa mã nguồn]

Rất lâu trước những văn tự cổ nhất, đã có những bức vẽ cho thấy một kỹ năng và kiến thức về toán học và đo thời hạn dựa trên sao trời. Ví dụ những nhà cổ sinh vật học đã mày mò ra những mảnh đất thổ hoàng trong một hang động ở Nam Phi được trang trí bởi những hình khắc hình học với thời hạn khoảng chừng 70.000 TCN. [ 3 ] Cũng những di khảo tiền sử được tìm thấy ở châu Phi và Pháp, thời hạn khoảng chừng giữa 35000 TCN và 20000 TCN, [ 4 ] cho thấy những cố gắng nỗ lực sơ khai nhằm mục đích định lượng thời hạn. [ 5 ]

Các bằng chứng còn tồn tại cho thấy việc đếm thời sơ khai chủ yếu là do phụ nữ, những người giữ các vật đánh dấu chu kì sinh học hàng tháng; ví dụ hai mươi tám, hai mươi chín, hoặc ba mươi vạch trên xương hoặc hòn đá, theo sau là một vạch cách biệt khác. Hơn nữa, các thợ săn đã có khái niệm về một, hai và nhiều cũng như không khi xem xét số bầy thú.[6][7]

Phương tiện liên quan tới Xương Ishango tại Wikimedia CommonsXương Ishango .Xương Ishango được tìm thấy ở thượng nguồn sông Nil ( phía bắc Cộng hòa Dân chủ Congo ), thuộc thời kì 20.000 TCN. Bản dịch thông dụng nhất của hòn đá cho ta thấy nó là vật chứng sớm nhất [ 4 ] biểu lộ một dãy những số nguyên tố và phép nhân Ai Cập cổ đại. Người Ai Cập vào thiên niên kỉ thứ 5 TCN đã vẽ những bức tranh về phong cách thiết kế hình học và khoảng trống. Người ta đã khẳng định chắc chắn những hòn đá tế thần ở Anh và Scotland từ thiên niên kỉ thứ 3 TCN, gồm có cả những sáng tạo độc đáo hình học như hình tròn, hình elíp và bộ ba Pythagore trong phong cách thiết kế của nó [ 8 ] .Nền toán học sớm nhất từng biết trong Ấn Độ cổ đại nằm vào khoảng chừng 3000 TCN – 2600 TCN ở nền văn minh thung lũng Indus ( nền văn minh Harappan ) của Bắc Ấn Độ và Pakistan, đã tăng trưởng một mạng lưới hệ thống những đơn vị chức năng đo Thung lũng Indus cổ đại sử dụng hệ cơ số 10, một công nghệ tiên tiến gạch đáng kinh ngạc sử dụng những tỉ lệ, những đường đi được đặt trên một góc vuông hoàn hảo nhất, và 1 số ít những hình hình học và phong cách thiết kế, gồm có hình hộp chữ nhật, thùng phi, hình nón, hình tròn trụ và những bức vẽ những hình tròn và hình tam giác cắt nhau và đồng qui. Các dụng cụ toán học tìm được gồm có một thước đo cơ số 10 với độ chia nhỏ và đúng chuẩn, một dụng cụ vỏ sò hoạt động giải trí như một chiếc com pa để đo góc trên mặt phẳng hoặc theo những bội của 40-360 độ, một dụng cụ vỏ sò để đo 8-12 phần của đường chân trời và khung trời, và một dụng cụ để đo vị trí của những sao nhằm mục đích mục tiêu khuynh hướng. Bản viết tay Indus vẫn chưa được giải nghĩa ; do đó ta biết được rất ít về những dạng viết của toán học Harappan. Các vật chứng khảo cổ đã làm những nhà sử học tin rằng nền văn minh này đã sử dụng hệ đếm cơ số 8 và đạt được những kiến thức và kỹ năng về tỉ lệ giữa chu vi của đường tròn so với bán kính của nó, do đó tính được số π. [ 9 ]

Toán học của người Maya[sửa|sửa mã nguồn]

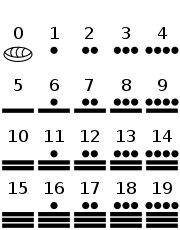Chữ số của người Maya, có số 0

Cùng phát triển với các nền văn minh Trung Mỹ khác, người Maya sử dụng hệ đếm nhị thập phân (vigesimal) và hệ ngũ phân (xem chữ số Maya). Hệ ngũ phân trên cơ sở so sánh với số ngón tay của một bàn tay, còn nhị thập phân là toàn bộ số ngón tay và ngón chân. Trong tiếng Quiche, từ chỉ số 20 là huvinak, có nghĩa là “toàn thân”. Ngoài ra, người Maya đã phát triển khái niệm “số 0” vào năm 357, sớm hơn châu Âu khoảng gần 900 năm. Văn bản cổ cho thấy, những người Maya, có nhu cầu công việc cộng vào hàng trăm triệu và số ngày lớn đòi hỏi phải có phương cách chính xác để thực hiện chúng. Kết quả tính toán về thiên văn học theo một không gian và thời gian dài là cực kỳ chính xác; bản đồ về sự vận động của Mặt Trăng và các hành tinh là ngang bằng hoặc vượt xa các văn minh khác quan sát vũ trụ bằng mắt thường.

Lịch MayaNgười Maya xác lập đúng chuẩn độ dài của một năm gồm 365 ngày, thời hạn Trái Đất quay hết một vòng quanh Mặt Trời, đúng chuẩn hơn rất nhiều lịch được châu Âu sử dụng vào thời đó ( lịch Gregory ). Có giả thiết cho rằng người Maya đã thừa kế cách tính lịch từ những nền văn minh cổ Zapotecs ( ở Mont Alban ) và Olmecs ( ở La venta và Tres Zapotes ). Tuy thế, người Maya lại không sử dụng độ dài giám sát thời hạn một năm vào lịch của họ. Người Maya sử dụng lịch ( gọi là lịch Maya ) trên cơ sở năm Mặt Trời với 365 ngày. Một năm Mặt Trời được chia thành 18 tháng, mỗi tháng có 20 ngày ( dùng hệ đếm cơ số 20 ), năm ngày còn lại được đưa vào cuối năm. Các ngày trong tháng được ghi bằng số thứ tự từ 0 đến 19 trước tên tháng ( 0 đến 4 cho tháng thiếu, cuối năm có 5 ngày ). Theo lịch này, những năm tiếp nối đuôi nhau nhau không ngừng, không có năm nhuận. Như vậy tác dụng là lịch sẽ bị rơi lệch lùi về một ngày trong vòng 4 năm. Khi so sánh với lịch Julius, dùng ở châu Âu từ thời Đế quốc La Mã cho đến tận thế kỷ 16, thì độ sai số cho một ngày là mỗi 128 năm ; với lịch Gregory văn minh, thì sai số sấp xỉ một ngày mỗi 3.257 năm .

Lịch của thầy bói

Ngày xưa, những người da đỏ Quiche, Ixil và Mam vẫn dùng lịch Maya truyền thống lịch sử với một năm có 260 ngày để Dự kiến tương lai. Để lý giải vì sao bộ lịch lại gồm 260 ngày, người ta đã phỏng vấn nhiều thầy bói ở Chichicastenango và Momstenango và phát hiện ra rằng : Việc chọn độ dài của năm này không phải do ngẫu nhiên mà là do tương thích với thời hạn mang thai của con người. Hệ đếm 20 cho phép chia một năm 260 ngày thành 13 tháng, mỗi tháng 20 ngày, tích hợp với một trong 20 tên gọi những con vật, những lực lượng tự nhiên, những ý niệm hay khái niệm mà ý nghĩa không còn lưu truyền đến thời nay .

Cận Đông cổ đại[sửa|sửa mã nguồn]

Bảng tính vạch trên đất sét YBC 7289 với chú giải chữ số văn minhToán học Babylon là ám chỉ bất kỳ nền toán học nào thuộc về dân cư Lưỡng Hà ( Iraq thời nay ) từ buổi đầu Sumer cho đến đầu thời kì Hy Lạp hóa. Nó được đặt tên là toán học Babylon là do vai trò TT của Babylon là nơi nghiên cứu và điều tra, nơi đã không còn sống sót sau thời kì Hy Lạp hóa. Các nhà toán học Babylon đã trộn với những nhà toán học Hy Lạp để tăng trưởng toán học Hy Lạp. Sau đó dưới Đế chế Arab, Iraq / Lưỡng Hà, đặc biệt quan trọng là Baghdad, một lần nữa trở thành TT điều tra và nghiên cứu quan trọng cho toán học Hồi giáo .Đối lập với sự thiếu thốn nguồn tài liệu của toán học Hy Lạp, sự hiểu biết về toán học Babylon của tất cả chúng ta là từ hơn 400 miếng đất sét khai thác được từ những năm 1850. Viết bằng ký tự Cuneiform, những miếng đất sét này được viết trong khi đất sét còn ẩm, và được nung cứng trong lò hoặc bằng nhiệt từ Mặt Trời. Một số trong đó có vẻ như là bài tập về nhà .Bằng chứng sớm nhất về những văn tự toán học là từ thời những người Sumer cổ đại, những người đã xây nên nền văn minh sớm nhất ở Lưỡng Hà. Họ đã tăng trưởng một hệ thống kê giám sát phức tạp từ 3000 TCN. Khoảng 2500 TCN trở lại trước, người Sumer đã viết những bảng nhân trên đất sét và giải những bài tập hình học và những bài toán chia. Dấu vết sớm nhất của hệ ghi số Babylon cũng là trong khoảng chừng thời hạn này. [ 10 ]Một lượng lớn những tấm đất sét đã được hồi sinh là vào lúc 1800 TCN tới 1600 TCN, và gồm có những chủ đề về phân số, đại số, phương trình bậc ba và bậc bốn, những giám sát về những bộ ba Pythagore ( xem Plimpton 322 ). [ 11 ] Các tấm này cũng gồm có cả bảng nhân, bảng lượng giác và những chiêu thức giải phương trình tuyến tính và phương trình bậc hai. Tấm đất sét YBC 7289 đã đưa ra một xê dịch của số √ 2 đúng chuẩn tới năm chữ số thập phân .Toán học Babylon được viết bằng hệ cơ số 60. Do việc này mà ngày này ta sử dụng 60 giây trong một phút, 60 phút trong một giờ và 360 ( 60 × 6 ) độ trong một vòng tròn. Các văn minh của người Babylon trong toán học tăng trưởng thuận tiện bởi số 60 có rất nhiều ước số. Cũng vậy, không giống người Ai Cập, Hy Lạp và La Mã, người Babylon có một hệ ghi số với cách viết số chia theo hàng, trong đó những chữ số viết ở cột bên trái bộc lộ giá trị lớn hơn, giống như hệ thập phân. Thế nhưng họ lại thiếu một ký hiệu tương tự của dấu thập phân, và do đó hàng trong cách viết số thường được suy ra từ ngữ cảnh .
Giấy cói Moskva Giấy cọ RhindToán học Ai Cập là ám chỉ toán học được viết dưới tiếng Ai Cập .Toán học Ai Cập cổ đại được lưu lại bởi nhân vật thần thoại cổ xưa Thoth, người được coi là đã đặt ra mẫu tự Ai Cập, mạng lưới hệ thống chữ số, toán học và thiên văn học, là vị thần của thời hạn .Từ thời kì Hy Lạp hóa, tiếng Hy Lạp đã sửa chữa thay thế tiếng Ai Cập trong ngôn từ viết của những nhà học giả Ai Cập, và từ thời gian này, toán học Ai Cập hợp nhất với toán học Hy Lạp và Babylon để tăng trưởng toán học Hy Lạp. Nghiên cứu toán học ở Ai Cập sau đó được liên tục dưới Đế chế Arab như là một phần của toán học Hồi giáo Trung Cổ, khi tiếng Ả Rập trở thành ngôn từ viết của những nhà học giả Ai Cập .Văn tự toán học cổ nhất tìm được cho tới nay là giấy cói Moskva, một văn tự bằng giấy cói của Vương quốc giữa Ai Cập vào khoảng chừng 2000 — 1800 mà thời nay ta gọi là ” bài toán chữ “, rõ ràng là chỉ để vui chơi. Một bài toán được coi là quan trọng ở mức nói riêng bởi nó đưa ra giải pháp tìm thể tích của một hình cụt : ” Nếu bạn biết : một hình chóp cụt có chiều cao 6, diện tích quy hoạnh đáy lớn 4, diện tích quy hoạnh đáy nhỏ 2. Bạn sẽ bình phương số 4 này, được 16. Bạn sẽ nhân đôi 4, được 8. Bạn sẽ bình phương 2, được 4. Bạn sẽ cộng 16, 8, và 4 được 28. Bạn sẽ lấy một phần ba của 6, được 2. Bạn nhân 28 với 2 được 56. Và 56 là số bạn cần tìm. ”
Giấy cọ Rhind ( khoảng chừng 1650 TCN ) là một văn bản toán học Ai Cập quan trọng khác, một hướng dẫn trong số học và hình học. Cùng với việc đưa ra những công thức diện tích quy hoạnh và phương pháp nhân, chia và thao tác với phân số đơn vị chức năng, nó cũng chứa những dẫn chứng về những kiến thức và kỹ năng toán học khác ( xem Egyptian Unit Fractions ) gồm có hợp số và số nguyên tố ; trung bình cộng, trung bình nhân và trung bình điều hòa ; và hiểu biết sơ bộ về sàng Eratosthenes và số tuyệt vời và hoàn hảo nhất. Nó cũng chỉ ra cách giải phương trình tuyến tính bậc một cũng như cấp số cộng và cấp số nhân .Cũng vậy, ba thành phần hình học có trong giấy cọ Rhind nói đến những kỹ năng và kiến thức đơn thuần nhất của hình học giải tích : ( 1 ) Đầu tiên và quan trọng nhất, làm thế nào để giao động số π đúng mực tới dưới một Xác Suất ; ( 2 ) thứ hai, một cố gắng nỗ lực cổ đại trong việc cầu phương hình tròn trụ ; ( 3 ) và thứ ba, sự sử dụng sớm nhất từng biết về lượng giác .Cuối cùng, giấy cọ Berlin cũng cho thấy người Ai Cập cổ đại hoàn toàn có thể giải phương trình đại số bậc hai .

Toán học Hy Lạp và Hy Lạp hóa cổ đại ( khoảng chừng 550 TCN-300 )[sửa|sửa mã nguồn]

Toán học Hy Lạp là ám chỉ toán học được viết bằng tiếng Hy Lạp khoảng chừng giữa 600 TCN và 450. [ 12 ] Các nhà toán học Hy Lạp sống ở những thành phố rải rác trên hàng loạt Địa Trung Hải, từ Ý tới Bắc Phi, nhưng lại thống nhất về văn hóa truyền thống và ngôn từ. Toán học Hy Lạp nhiều lúc được gọi là toán học Hellenistic ( Hy Lạp hóa ) .Toán học Hy Lạp đã trở nên phức tạp hơn rất nhiều so với những nền văn hóa truyền thống trước đó. Tất cả những ghi chép còn sống sót của những nền toán học tiền Hy Lạp đều cho thấy việc sử dụng suy luận quy nạp, nghĩa là, những quan sát liên tục được sử dụng để lập nên những phép đo dựa trên kinh nghiệm tay nghề. Người Hy Lạp sử dụng lý luận logic để đạt được những Tóm lại từ những định nghĩa và tiên đề [ 13 ] .
Toán học Hy Lạp có vẻ như mở màn với Thales ( khoảng chừng 624 – khoảng chừng 546 TCN ) và Pythagoras ( khoảng chừng 582 – khoảng chừng 507 TCN ). Mặc dù tầm ảnh hưởng tác động không còn, họ hoàn toàn có thể vẫn tăng trưởng ý tưởng sáng tạo từ toán học Ai Cập, Babylon, và hoàn toàn có thể cả Ấn Độ. Theo thần thoại cổ xưa, Pythagoras đã chu du tới Ai Cập để học toán học, hình học, và thiên văn từ những đạo sĩ Ai Cập .Thales đã sử dụng hình học để giải những bài toán như thể tính độ cao của những hình chóp và khoảng cách từ những tàu tới bờ biển. Pythagoras được coi là người tiên phong đưa ra chứng tỏ cho định lý Pythagore, mặc dầu phát biểu của định lý đã đi qua một chặng đường lịch sử dân tộc dài. Trong lời phản hồi về Euclid, Proclus phát biểu rằng Pythagoras đã diễn đạt định lý mang tên ông và dựng nên bộ ba Pythagore một cách đại số hơn là hình học. Trường học của Plato có câu khẩu hiệu : ” Không để những thứ nông cạn trong hình học vào đây. “

Học thuyết Pythagoras đã khám phá ra sự tồn tại của các số hữu tỉ. Eudoxus (408 – khoảng 355 TCN) đã phát minh ra phương pháp vét cạn, tiền thân của khái niệm hiện đại tích phân. Aristotle (384 – khoảng 322 TCN) đã lần đầu viết ra các luật về logic. Euclid (khoảng 300 TCN) là ví dụ sớm nhất của một khuôn mẫu mà vẫn còn được sử dụng cho đến ngày nay, định nghĩa, tiên đề, định lý, chứng minh. Ông cũng nghiên cứu về các đường conic. Cuốn sách của ông, Cơ bản, được tất cả những người có học biết đến ở phương Tây cho đến giữa thế kỉ 20.[14] Thêm vào các định lý quen thuộc của hình học, như định lý Pythagore, Cơ bản còn có cả chứng minh rằng căn bậc hai của hai là số vô tỉ và có vô hạn số nguyên tố. Sàng Eratosthenes (khoảng 230 TCN) đã được sử dụng để tìm các số nguyên tố. Với người Hy Lạp, toán học đã vượt lên cả việc ghi chép. Những nhà toán học có tên tuổi tới nay đã để lại những định lý, tiên đề có giá trị khái quát cao trong cuộc sống và đặc biệt đối với lĩnh vực toán học

Một số người nói rằng người vĩ đại nhất trong các nhà toán học Hy Lạp, nếu không muốn nói là mọi thời đại, là Archimedes xứ Syracuse (287—212 TCN) xứ Syracuse[cần dẫn nguồn]. Theo như Lucius Mestrius Plutarchus, ở tuổi 75, trong khi đang vẽ các công thức toán học ở trên cát, ông đã bị một tên lính La Mã dùng giáo đâm chết. Roma cổ đại để lại ít bằng chứng về sự quan tâm vào toán học lý thuyết.

Toán học Ấn Độ cổ đại ( khoảng chừng 1500 TCN-200 CN )[sửa|sửa mã nguồn]

Toán học Vệ Đà bắt đầu vào đầu thời kì Đồ Sắt, với Shatapatha Brahmana (khoảng thế kỉ 9 TCN), trong đó có xấp xỉ số π chính xác tới 2 chữ số thập phân[15] và Sulba Sutras (khoảng 800-500 TCN) là các văn bản hình học sử dụng số vô tỉ, số nguyên tố, luật ba, và căn bậc ba; tính căn bậc hai của 2 tới năm chữ số thập phân; đưa ra phương pháp cầu phương hình tròn, giải phương trình tuyến tính và phương trình bậc hai; phát triển bộ ba Pythagore theo phương pháp đại số, phát biểu và nêu chứng minh cho Định lý Pythagore.

Pāṇini (khoảng thế kỉ 5 TCN) đã lập công thức cho ngữ pháp của tiếng Phạn. Ký hiệu của ông tương tự với ký hiệu toán học, và sử dụng các ngôn luật, các phép biến đổi, đệ quy với độ phức tạp đến mức ngữ pháp của ông có sức mạnh tính toán ngang với máy Turing. Công trình của Panini cũng đi trước cả lý thuyết hiện đại ngữ pháp hình thức (formal grammar) (có vai trò quan trọng trong điện toán), trong khi dạng Panini-Backus được sử dụng bởi những ngôn ngữ lập trình hiện đại nhất lại rất giống với luật ngữ pháp của Panini. Pingala (khoảng thế kỉ thứ 3 đến thứ nhất TCN) trong bản luận thuyết của mình về thi pháp đã sử dụng một phương pháp ứng với hệ nhị phân. Thảo luận của ông về tổ hợp của các phách, tương ứng với định lý nhị thức. Công trình của Pingala cũng chứa các ý tưởng cơ bản của các số Fibonacci (được gọi là mātrāmeru). Văn bản Brāhmī được phát triển ít nhất từ thời triều Maurya vào thế kỉ 4 TCN, với những bằng chứng khảo cổ học cho thấy nó xuất hiện vào khoảng 600 TCN. Chữ số Brahmi ở vào khoảng thế kỉ 3 TCN.

Giữa năm 400 TCN và 200 CN, các nhà toán học Jaina bắt đầu nghiên cứu toán học với mục đích duy nhất cho toán học. Họ là những người đầu tiên phát triển transfinite number, lý thuyết tập hợp, logarit, các định luật cơ bản của lũy thừa, phương trình bậc ba, phương trình bậc bốn, dãy số và dãy cấp số, hoán vị và tổ hợp, bình phương và lấy xấp xỉ căn bậc hai, và hàm mũ hữu hạn và vô hạn. Bản thảo Bakshali được viết giữa 200 TCN và 200 bao gồm cách giải hệ phương trình tuyến tính tới năm ẩn, nghiệm phương trình bậc hai, cấp số cộng và cấp số nhân, dãy phức hợp, phương trình vô định bậc hai, phương trình không mẫu mực, và sự sử dụng số 0 và số âm. Các tính toán chính xác cho số vô tỉ đã được tìm ra, bao gồm tính căn bậc hai của các số tới bao nhiêu chữ số sau dấu phẩy tùy thích (từ 11 chữ số trở lên).

Toán học Trung Quốc cổ đại ( khoảng chừng 1300 TCN-200 CN )[sửa|sửa mã nguồn]

Cửu chương toán thuật

Bắt đầu từ thời nhà Thương (1600 TCN— 1046 TCN), toán học Trung Quốc sớm nhất còn tồn tại bao gồm các số được khắc trên mai rùa.[16][17] Các số này sử dụng hệ cơ số 10, vì vậy số 123 được viết (từ trên xuống dưới) bằng một ký hiệu cho số 1 rồi đến một ký hiệu hàng trăm, sau đó là ký hiệu cho số 2 rồi đến ký hiệu hàng chục, sau đó là số 3. Đây là hệ cơ số tiến bộ nhất trên thế giới vào thời điểm đó và cho phép tính toán được thực hiện bởi bàn tính. Thời điểm phát minh ra bàn tính không rõ, nhưng tài liệu cổ nhất vào 190 trong Lưu ý về the Art of Figures viết bởi Xu Yue. Bàn tính có thể đã được sử dụng trước thời điểm này.

Ở Trung Quốc, vào 212 TCN, vua Tần Thủy Hoàng đã ra lệnh đốt toàn bộ sách trong nước. Cho dù lệnh này không được tuân thủ trọn vẹn, nhưng ta vẫn biết rất ít về toán học Trung Quốc cổ đại .Từ triều Tây Chu ( từ 1046 ), khu công trình toán học cổ nhất còn sống sót sau cuộc đốt sách là Kinh Dịch, trong đó sử dụng 64 quẻ 6 hào cho mục tiêu triết học hay tâm linh. Các hào là những bộ hình vẽ gồm những đường gạch đậm liền hoặc đứt nét, đại diện thay mặt cho dương và âm .

Sau cuộc đốt sách, nhà Hán (202 TCN) – 220 đã lập các công trình về toán học có thể là phát triển dựa trên các công trình mà hiện nay đã mất. Phần quan trọng nhất trong số đó là Cửu chương toán thuật, tiêu đề của nó xuất hiện trước 179 CN, nhưng là nằm trong các tiêu đề khác tồn tại trước đó. Nó bao gồm 264 bài toán chữ, chủ yếu là nông nghiệp, thương nghiệp, áp dụng của hình học để đo chiều cao và tỉ lệ trong các chùa chiền, công trình, thăm dò, và bao gồm các kiến thức về tam giác vuông và số π. Nó cũng áp dụng nguyên lý Cavalieri (Cavalieri’s principle) về thể tích hơn một nghìn năm trước khi Cavalieri đề xuất ở phương Tây. Nó đặt ra chứng minh toán học cho Định lý Pythagore, và công thức toán học cho phép khử Gauss. Công trình này đã được chú thích bởi Lưu Huy (Liu Hui) vào thế kỉ thứ 3 trước Công nguyên.

Ngoài ra, các công trình toán học của nhà thiên văn học, nhà phát minh Trương Hành (Zhang Heng, 78-139) đã có công thức cho số pi, khác so với tính toán của Lưu Huy. Trương Hành sử dụng công thức của ông cho số pi để tính thể tích hình cầu V theo đường kính D.

V=9 16 { \ displaystyle { \ tfrac { 9 } { 16 } } }3 + 1 16 { \ displaystyle { \ tfrac { 1 } { 16 } } }3 = 5 8 { \ displaystyle { \ tfrac { 5 } { 8 } } }3

Người Trung Quốc cũng sử dụng biểu đồ tổng hợp phức còn gọi là ‘ hình vuông vắn thần kì ‘, được miêu tả trong những thời kì cổ đại và được hoàn hảo bởi Dương Huy ( 1238 – 1398 ) .

Toán học Trung Quốc cổ xưa ( khoảng chừng 400 – 1300 )[sửa|sửa mã nguồn]

Tổ Xung Chi ( Zu Chongzhi ) ( thế kỉ 5 ) vào thời Nam Bắc Triều đã tính được giá trị của số π đúng mực tới bảy chữ số thập phân, trở thành tác dụng đúng chuẩn nhất của số π trong gần 1000 năm .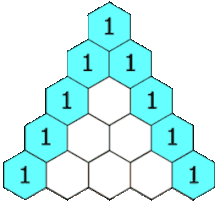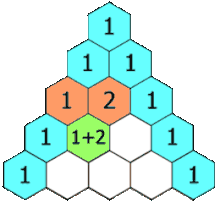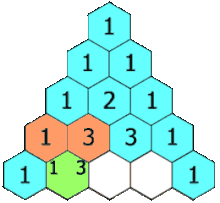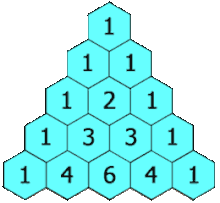
Tam giác PascalTrong hàng nghìn năm sau nhà Hán, mở màn từ nhà Đường và kết thúc vào nhà Tống, toán học Trung Quốc tăng trưởng thịnh vượng, nhiều bài toán phát sinh và xử lý trước khi Open ở châu Âu. Các tăng trưởng trước hết được phát sinh ở Trung Quốc, và chỉ rất lâu sau mới được biết đến ở phương Tây, gồm có số âm, định lý nhị thức, chiêu thức ma trận để giải hệ phương trình tuyến tính và [ [ Định lý số dư Trung Quốc ] ] về nghiệm của hệ phương trình đồng dư bậc nhất .

• Số âm được đề cập đến trong bảng cửu chương từ thời nhà Hán, 200TCN[18]
• Định lý nhị thức và tam giác Pascal được Yang Hui nghiên cứu từ thế kỷ 13
• Ma trận được người Trung Quốc nghiên cứu và thành lập bảng ma trận từ những năm 650 TCN[19]

Người Trung Quốc cũng đã tăng trưởng tam giác Pascal và luật ba rất lâu trước khi nó được biết đến ở châu Âu. Ngoài Tổ Xung Chi ra, một số ít nhà toán học nổi tiếng ở Trung Quốc thời kì này là Nhất Hành, Shen Kuo, Chin Chiu-Shao, Zhu Shijie, và những người khác. Nhà khoa học Shen Kuo sử dụng những bài toán tương quan đến giải tích, lượng giác, khí tượng học, hoán vị, và nhờ đó thống kê giám sát được lượng khoảng trống địa hình hoàn toàn có thể sử dụng với những dạng trận đánh đơn cử, cũng như doanh trại giữ được lâu nhất hoàn toàn có thể với lượng phu hoàn toàn có thể mang lương cho chính họ và binh sĩ .Thậm chí sau khi toán học châu Âu mở màn nở rộ trong thời kì Phục hưng, toán học châu Âu và Trung Quốc khác nhau về truyền thống cuội nguồn, với sự sụt giảm của toán học Trung Quốc, cho tới khi những nhà truyền đạo Thiên Chúa giáo mang những ý tưởng sáng tạo toán học tới và đi giữa hai nền văn hóa truyền thống từ thế kỉ 16 đến thế kỉ 18 .

Toán học Ấn Độ cổ xưa ( khoảng chừng 400 – 1600 )[sửa|sửa mã nguồn]

Cuốn Surya Siddhanta (khoảng 400) giới thiệu các hàm lượng giác như sin, cosin, và sin ngược, và đưa ra các luật để xác định chuyển động chính xác của các thiên thể, tuân theo vị trí thật của chúng trên bầu trời. Thời gian vũ trụ tuần hoàn được giải thích trong cuốn sách, được sao chép từ một công trình trước đó, tương ứng với năm thiên văn với 365,2563627 ngày, chỉ dài hơn 1,4 giây so với giá trị hiện đại. Công trình này đã được dịch ra tiếng Ả Rập và Latin trong thời Trung Cổ.

Aryabhata vào năm 499 giới thiệu hàm versin, đưa ra bản sin đầu tiên, phát triển các kĩ thuật và thuật toán của đại số, vô cùng nhỏ, phương trình vi phân, và đạt được lời giải hoàn chỉnh cho các phương trình tuyến tính bằng một phương pháp ứng với phương pháp hiện đại, cùng với các tính toán thiên văn chính xác dựa trên thuyết nhật tâm. Một bản dịch tiếng Ả Rập của cuốn Aryabhatiya có từ thế kỉ 8, sau đó là bản Latin vào thế kỉ 13. Ông cũng tính giá trị π chính xác tới bốn chữ số sau dấu phẩy. Madhava sau đó vào thế kỉ 14 đã tính giá tị của số π chính xác tới chữ số thập phân thứ mười một là 3.14159265359.

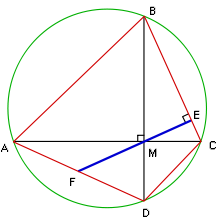A F = F D { \ displaystyle AF = FD }Chứng minh của Brahmagupta rằng

Vào thế kỉ 7, Brahmagupta đã đưa ra định lý Brahmagupta, đẳng thức Brahmagupta và công thức Brahmagupta lần đầu tiên, trong cuốn Brahma-sphuta-siddhanta, ông đã giải thích một cách rõ ràng cách sử dụng số 0 vừa là ký hiệu thay thế vừa là chữ số thập phân và giải thích hệ ghi số Hindu-Arabic. Theo một bản dịch của văn bản tiếng Ấn về toán học này (khoảng 770), các nhà toán học Hồi giáo đã được giới thiệu hệ ghi số này, mà họ gọi là hệ ghi số Ả Rập. Các nhà học giả Hồi giáo đã mang kiến thức về hệ ghi số này tới châu Âu trước thế kỉ 12, và nó đã thay thế toàn bộ các hệ ghi số cũ hơn trên toàn thế giới. Vào thế kỉ 10, bình luận của Halayudha về công trình của Pingala bao gồm một nghiên cứu về dãy Fibonacci và tam giác Pascal, và mô tả dạng của một ma trận.

Vào thế kỉ 12, Bhaskara lần đầu tiên đặt ra ý tưởng về giải tích vi phân, cùng với khái niệm về đạo hàm, hệ số vi phân và phép lấy vi phân. Ông cũng đã chứng minh định lý Rolle (một trường hợp đặc biệt của định lý giá trị trung bình), nghiên cứu phương trình Pell, và xem xét đạo hàm của hàm sin. Từ thế kỉ 14, Madhava và các nhà toán học khác của Trường phái Kerala, phát triển thêm các ý tưởng của ông. Họ đã phát triển các khái niệm về thống kê toán học và số dấu phẩy động, và khái niệm căn bản cho việc phát triển của toàn bộ giải tích, bao gồm định lý giá trị trung bình, tích phân từng phần, quan hệ giữa diện tích dưới một đường cong và nguyên hàm của nó, kiểm tra tính hội tụ, phương pháp lặp để giải nghiệm phương trình phi tuyến, và một số chuỗi vô hạn, chuỗi hàm mũ, chuỗi Taylor và chuỗi lượng giác. Vào thế kỉ 16, Jyeshtadeva đã củng cố thêm rất nhiều định lý và phát triển của Trường Kerala trong cuốn Yuktibhasa, văn bản về đạo hàm đầu tiên trên thế giới, cũng đưa ra khái niệm tích phân. Phát triển toán học ở Ấn Độ chững lại từ cuối thế kỉ 16 do các rắc rối về chính trị.

Toán học Ả Rập và đạo Hồi ( khoảng chừng 800 – 1500 )[sửa|sửa mã nguồn]

Đế chế Ả Rập Đạo Hồi được thiết lập trên hàng loạt Trung Đông, Trung Á, Bắc Phi, Iberia, và một số ít phần của Ấn Độ trong thế kỉ 8 đã tạo nên những góp sức quan trọng cho toán học. Mặc dù phần đông những văn bản Đạo Hồi được viết bằng tiếng Ả Rập, chúng không trọn vẹn được viết bởi những người Ả Rập, rất hoàn toàn có thể do vị thế của Hy Lạp trong quốc tế Hellenistic, tiếng Ả Rập được sử dụng như thể ngôn từ viết của những học giả không phải người Ả Rập trong quốc tế Đạo Hồi thời bấy giờ. Một số trong những nhà toán học Đạo Hồi quan trọng nhất là người Ba Tư .

Muhammad ibn Mūsā al-Khwārizmī, một nhà toán học và thiên văn học Ba Tư thế kỉ thứ 9, đã viết một vài cuốn sách quan trọng về hệ ghi số Hindu-Arabic và về các phương pháp giải phương trình. Cuốn sách của ông Về tính toán với hệ ghi số Hindu, được viết khoảng năm 825, cùng với công trình của nhà toán học Ả Rập Al-Kindi, là những công cụ trong việc truyền bá toán học Ấn Độ và hệ ghi số Hindu-Arabic tới phương Tây. Từ algorithm (thuật toán) bắt nguồn từ sự Latin hóa của tên ông, Algoritmi, và từ algebra (đại số) từ tên của một trong những công trình của ông, Al-Kitāb al-mukhtaṣar fī hīsāb al-ğabr wa’l-muqābala (Cuốn cẩm nang về tính toán bằng hoàn thiện và cân đối). Al-Khwarizmi thường được gọi là “cha đẻ của đại số”, bởi sự bảo tồn các phương pháp đại số cổ đại của ông và các cống hiến của ông đối với lĩnh vực này.[20] Các phát triển thêm của đại số được thực hiện bởi Abu Bakr al-Karaji (953—1029) trong học thuyết của ông al-Fakhri, ở đó ông mở rộng các quy tắc để thêm cả lũy thừa số nguyên và nghiệm nguyên vào các đại lượng chưa biết. Vào thế kỉ 10, Abul Wafa đã dịch công trình của Diophantus thành tiếng Ả Rập và phát triển hàm tang.

Chứng minh tiên phong bằng quy nạp toán học Open trong một cuốn sách viết bởi Al-Karaji khoảng chừng 1000 CN, người đã sử dụng nó để chứng tỏ định lý nhị thức, tam giác Pascal, và tổng của những lập phương nguyên. [ 21 ] Nhà nghiên cứu và điều tra lịch sử dân tộc toán học, F. Woepcke, [ 22 ] đã ca tụng Al-Karaji là ” người tiên phong ra mắt những định lý của những phép tính đại số. “Ibn al-Haytham là người tiên phong bắt nguồn sử dụng những công thức tính tổng của lũy thừa bậc bốn sử dụng chiêu thức quy nạp, từ đó tăng trưởng thành giải pháp tính tích phân. [ 23 ]

Omar Khayyam, nhà thơ thế kỉ 12, cũng là một nhà toán học, viết Bàn luận về những khó khăn của Euclid, một cuốn sách về các thiếu sót của cuốn Cơ sở của Euclid, đặc biệt là tiên đề về đường thẳng song song, và do đó ông đặt ra nền móng cho hình học giải tích và hình học phi Euclid. Ông cũng là người đầu tiên tìm ra nghiệm hình học của phương trình bậc ba. Ông cũng có ảnh hưởng lón trong việc cải tổ lịch.

Nasir al-Din Tusi và bảng IlkhanicBút tích của Jamshīd al-KāshīNhà toán học Ba Tư Nasir al-Din Tusi ( Nasireddin ) vào thế kỉ 13 đã tạo nên những bước tiến trong lượng giác hình cầu. Ông cũng viết những khu công trình có ảnh hưởng tác động lớn tới tiên đề về đường thẳng song song của Euclid .

Vào thế kỉ 15, Ghiyath al-Kashi đã tính giá trị số π tới chữ số thập phân thứ 16. Kashi cũng có một thuật toán cho phép tính căn bậc n, là trường hợp đặc biệt của các phương pháp đã đưa ra hàng thế kỉ sau bởi Ruffini và Horner. Các nhà toán học Hồi giáo đáng lưu ý khác bao gồm al-Samawal, Abu’l-Hasan al-Uqlidisi, Jamshid al-Kashi, Thabit ibn Qurra, Abu Kamil và Abu Sahl al-Kuhi.

Đến thời Đế chế Ottoman ( từ thế kỉ 15 ), sự tăng trưởng của toán học Hồi giáo bị chững lại. Điều này song song với sự chững lại của toán học khi người Roma chinh phục được quốc tế Hellenistic .

John J. O’Connor và Edmund F. Robertson viết trong cuốn MacTutor History of Mathematics archive:

“Những nghiên cứu gần đây vẽ ra một bức tranh mới về những thứ mà ta nợ toán học Đạo Hồi. Hiển nhiên rất nhiều các ý tưởng nghĩ ra trước đó đã trở thành những khái niệm tuyệt vời do toán học châu Âu của thế kỉ mười sáu, mười bảy, mười tám theo ta biết là đã được phát triển bởi các nhà toán học Ả Rập/Đạo Hồi bốn thế kỉ trước đó. Trong nhiều khía cạnh, toán học được nghiên cứu ngày nay còn gần hơn về phong cách đối với những thứ đó của toán học Đạo Hồi hơn là những thức của toán học Hellenistic.”

Toán học châu Âu Trung cổ ( khoảng chừng 300 – 1400 )[sửa|sửa mã nguồn]

Mối quan tâm đến toán học của châu Âu Trung cổ là do nhiều lý do rất khác so với của các nhà toán học hiện đại. Một lý do đó là niềm tin rằng toán học là chìa khóa để hiểu được thứ bậc trong tự nhiên, thường được đánh giá trong cuộc đối thoại Timaeus của Plato và chuyến đi lớn mà Chúa đã “sắp xếp tất cả mọi thứ theo kích thước, số lượng, và cân nặng” (Wisdom 11:21).

Thời kì Trung cổ sơ khai ( khoảng chừng 300 – 1100 )[sửa|sửa mã nguồn]

Boethius và các học trò

Boethius (480–524) đã dành một nơi cho toán học trong môn học khi ông đưa ra khái niệm “quadrivium” (tiếng Latinh: bốn con đường) để chỉ các môn số học, hình học, thiên văn học, và âm nhạc. Ông viết De institutione arithmetica, dịch thoáng nghĩa từ tiếng Hy Lạp tiêu đề của cuốn Introduction to Arithmetic của Nicomachus; De institutione musica, cũng phát triển từ gốc Hy Lạp; và một loạt các đoạn lấy từ cuốn Cơ sở của Euclid. Công trình của ông mang tính lý thuyết hơn là thực hành, và là công trình nền tảng của toán học cho đến khi các công trình toán học của Hy Lạp và A Rập được phục hồi.[24][25]

Sự hồi sinh của toán học tại châu Âu ( 1100 – 1400 )[sửa|sửa mã nguồn]

Fibonacci

Vào thế kỉ 12, các nhà học giả châu Âu đã chu du đến Tây Ban Nha và Sicilia để tìm các văn bản tiếng A Rập, trong số chúng là cuốn Al-Jabr wa-al-Muqabilah của Al-Khwarizmi, được dịch thành tiếng Latinh bởi Robert of Chester và văn bản đầy đủ của cuốn Cơ sở của Euclid, được dịch thành rất nhiều phiên bản bởi Adelard of Bath, Herman of Carinthia, và Gerard of Cremona.[26][27]

Những nguồn mới này lóe lên một thời kì hồi sinh của toán học. Fibonacci, vào đầu thế kỉ 13, đưa ra khu công trình toán học quan trọng tiên phong ở châu Âu kể từ thời của Eratosthenes, một khoảng chừng thời hạn hơn một nghìn năm. Thế kỉ mười bốn đã tận mắt chứng kiến sự tăng trưởng của những khái niệm toán học mới để xử lý một loạt bài toán. [ 28 ] Một nghành nghề dịch vụ quan trọng góp sức cho sự tăng trưởng của toán học đó là nghiên cứu và phân tích những hoạt động địa phương .Thomas Bradwardine đưa ra rằng tốc độ ( V ) tăng theo tỉ lệ số học khi tỉ số của lực ( F ) với lực cản ( R ) tăng theo số mũ. Bradwardine miêu tả điều này bằng một loạt những ví dụ đơn cử, nhưng mặc dầu lôgarít thời đó chưa Open, ta hoàn toàn có thể màn biểu diễn Tóm lại của ông dưới dạng V = log ( F / R ). [ 29 ] Phân tích của Bradwardine là một ví dụ của việc quy đổi kĩ thuật toán học được sử dụng bởi al-Kindi và Arnald of Villanova để định tính thực chất của thuốc trộn thành một bài toán vật lý khác. [ 30 ]

Là một người trong nhóm Oxford Calculators vào thế kỉ 14, William Heytesbury, thiếu giải tích vi phân và khái niệm giới hạn, đã đưa ra việc đo vận tốc tức thời “bằng con đường mà có thể được mô tả bởi một vật thể nếu… nó được dịch chuyển đi theo cùng một tốc độ mà với điều đó nó được di chuyển trong thời khắc đã cho”.[31]

Heytesbury và những người khác đã xác lập bằng toán học khoảng cách đi được của một vật thể hoạt động có tần suất không đổi ( mà ta hoàn toàn có thể giải thuận tiện bằng Tích phân ), nói rằng ” một vật thể hoạt động mà nhận tốc độ giảm hoặc tăng không đổi sẽ đi trong một thời hạn nào đó cho trước một khoảng cách trọn vẹn bằng với khoảng cách ấy mà sẽ đi được nếu nó đang hoạt động liên tục trong cùng một thời hạn với vận tốc trung bình “. [ 32 ]
Nicole Oresme
Oresme đã đi trước Galileo trong việc điều tra và nghiên cứu tích phân

Nicole Oresme tại Đại học Paris và Giovanni di Casali người Italia độc lập với nhau đưa ra biểu diễn đồ thị của quan hệ này, thêm vào diện tích dưới đường thẳng biểu thị gia tốc không đổi, thể hiện tổng quãng đường đi được.[33] Trong một buổi thảo luận sau đó về cuốn Hình học của Euclid, Oresme đưa ra một phân tích chi tiết tổng quát trong đó ông nói rằng một vật thể sẽ nhận được trong mỗi số gia của thời gian một số gia của bất kì tính chất nào mà tăng như số lẻ. Do Euclid đã chứng minh tổng của các số lẻ là các số chính phương, tổng các tính chất đạt được bởi vật thể tăng theo bình phương thời gian.[34]

Toán học văn minh sơ khai châu Âu[sửa|sửa mã nguồn]

Ở châu Âu vào buổi bình minh của thời kì Phục Hưng, toán học vẫn còn bị hạn chế bởi các ký hiệu cồng kềnh sử dụng hệ ghi số La Mã và diễn đạt các quan hệ bằng từ ngữ, hơn là bằng ký hiệu: không có dấu cộng, không có dấu bằng, và không sử dụng x thay cho đại lượng chưa biết.

Vào thế kỉ 16 các nhà toán học châu Âu bắt đầu tạo nên những bước tiến mới mà không cần biết đến những nơi khác trên thế giới, tới mức như ngày nay. Bước tiến đầu tiên trong số đó là nghiệm tổng quát của phương trình bậc ba, thông thường được ghi công cho Scipione del Ferro vào khoảng 1510, nhưng xuất bản lần đầu tiên bởi Johannes Petreius ở Nürnberg trong cuốn Ars magna của Gerolamo Cardano, trong đó cũng có nghiệm tổng quát của phương trình bậc bốn từ học trò của Cardano Lodovico Ferrari.

Từ thời điểm này, toán học phát triển nhanh chóng, bổ trợ cho và lấy lợi ích từ các tiến bộ mới cùng thời của vật lý học. Quá trình này càng được thúc đẩy bởi những tiến bộ trong ngành in. Cuốn sách toán học sớm nhất được in là cuốn Theoricae nova planetarum của G. v. Peuerbach vào 1472, theo sau là một cuốn sách về số học thương mại Treviso Arithmetic năm 1478 và cuốn sách toán học thực sự của Euclid, cuốn Cơ sở được in và xuất bản bởi Ratdolt năm 1482.

Do nhu cầu cấp thiết về định hướng và vẽ bản đồ chính xác cho những khu vực rộng lớn, lượng giác đã phát triển thành một ngành lớn của toán học. Bartholomaeus Pitiscus là người đầu tiên sử dụng từ Trigonometria (lượng giác) trong cuốn sách cùng tên của ông vào năm 1595. Bảng sin và cosin của Regiomontanus được xuất bản vào 1533.[35]

• Regiomontanus, Đức
• François Viète, Pháp

Đến cuối thế kỉ, nhờ có Johannes Müller von Königsberg ( 1436 – 1476 ) và François Viète ( 1540 – 1603 ), cùng với những người khác, mà toán học đã được viết bằng hệ ghi số Hindu-Arabic và theo một dạng mà không quá khác xa so với những ký hiệu sử dụng thời nay .

Thế kỉ 17[sửa|sửa mã nguồn]

Thế kỉ 17 tận mắt chứng kiến sự bùng nổ chưa từng thấy của những ý tưởng sáng tạo toán học và khoa học trên toàn châu Âu .Galileo, một người Italia, đã quan sát những Mặt Trăng của Sao Mộc trên quỹ đạo quanh hành tinh đó, sử dụng kính viễn vọng dựa trên một đồ chơi nhập khẩu từ Hà Lan .
Mô tả của Tychoo về quỹ đạo của Mặt Trăng, Mặt Trời và những hành tinhTycho Brahe, ở vương quốc Đan Mạch, đã tích lũy một lượng lớn những tài liệu toán học miêu tả những vị trí của những hành tinh trên khung trời. Học trò của ông, nhà toán học người Đức Johannes Kepler, khởi đầu thao tác với những tài liệu này. Một phần do tại muốn giúp Kepler trong việc thống kê giám sát, John Napier, ở Scotland, là người tiên phong nghiên cứu và điều tra logarit tự nhiên. Kepler thành công xuất sắc trong việc lập công thức toán học những định luật của hoạt động hành tinh. Hình học giải tích được tăng trưởng bởi René Descartes ( 1596 – 1650 ), một nhà toán học và triết học người Pháp, đã được cho phép những quỹ đạo này hoàn toàn có thể vẽ được trên đồ thị, trong hệ toạ độ Descartes. Xây dựng dựa trên những khu công trình đi trước bởi rất nhiều nhà toán học, Isaac Newton, người Anh, đã tò mò ra những định luật của vật lý để lý giải định luật Kepler, và cùng đưa đến một khái niệm giờ đây ta gọi là giải tích. Một cách độc lập, Gottfried Wilhelm Leibniz, ở Đức, đã tăng trưởng giải tích và rất nhiều những ký hiệu giải tích vẫn còn được sử dụng cho đến ngày này. Khoa học và toán học đã trở thành một nỗ lực quốc tế, nhanh gọn lan ra toàn quốc tế. [ 36 ]Thêm vào ứng dụng của toán học so với ngành thần học, toán học ứng dụng mở màn lan rộng ra ra những nghành mới khác, với những lá thư giữa Pierre de Fermat và Blaise Pascal. Pascal và Fermat đã đặt nền móng cho việc điều tra và nghiên cứu triết lý Tỷ Lệ và những định luật tổng hợp tương ứng trong những bàn luận của họ về trò đánh bạc. Pascal, với Sự đánh cuộc Pascal, đã nỗ lực sử dụng triết lý Tỷ Lệ mới của mình để tranh luận về một đời sống theo tôn giáo, trong thực tiễn là dù Xác Suất thành công xuất sắc có nhỏ đi nữa, phần lợi vẫn là vô cùng. Trong thực trạng này, điều đó đã dự báo trước sự tăng trưởng của triết lý thỏa dụng ở nửa sau thế kỉ 18-19

Thế kỉ 18[sửa|sửa mã nguồn]

Như ta đã thấy, sự hiểu biết về những số tự nhiên 1, 2, 3, … còn trước bất kể văn bản viết nào. Những nền văn minh sớm nhất – ở Lưỡng Hà, Ai Cập, Ấn Độ và Trung Quốc – đều đã biết đến số học .Một cách để xem xét sự tăng trưởng của rất nhiều hệ toán học tân tiến khác nhau là xem những hệ mới được nghiên cứu và điều tra để vấn đáp những câu hỏi về số học của những hệ cũ hơn. Trong thời tiền sử, phân số vấn đáp được câu hỏi : số nào, khi nhân với 3, thì được hiệu quả là 1. Ở Ấn Độ và Trung Quốc, và rất lâu sau ở Đức, những số âm được tăng trưởng đề vấn đáp thắc mắc : bạn nhận được hiệu quả là gì khi lấy 1 số ít nhỏ trừ đi số lớn. Việc phát minh ra số không hoàn toàn có thể là để vấn đáp thắc mắc : bạn nhận được tác dụng là gì khi trừ 1 số ít cho chính nó .Một câu hỏi tự nhiên khác là : căn bậc hai của số hai là kiểu số gì ? Người Hy Lạp đã biết rằng nó không phải một phân số, và câu hỏi này đã đóng vai trò quan trọng trong việc tăng trưởng liên phân số. Nhưng một câu vấn đáp tốt hơn Open cùng với sự phát minh ra chữ số thập phân, tăng trưởng bởi John Napier ( 1550 – 1617 ) và được hoàn hảo sau đó bởi Simon Stevin. Sử dụng những chữ số thập phân, và một sáng tạo độc đáo mà tiên đoán trước được khái niệm về số lượng giới hạn, Napier cũng đã nghiên cứu và điều tra một hằng số mới, mà Leonhard Euler ( 1707 – 1783 ) đã đặt tên là số e. [ 37 ]

Euler có rất nhiều ảnh hưởng tới việc chuẩn hóa các ký hiệu và thuật ngữ toán học. Ông đã đặt tên căn bậc hai của âm một bằng ký hiệu i. Ông cũng phổ biến việc sử dụng chữ cái Hy Lạp

π

{\displaystyle \pi }

để chỉ tỉ số của chu vi một đường tròn đối với đường kính của nó. Sau đó ông còn phát triển thêm một trong những công thức đáng chú ý nhất của toán học:

e i π + 1 = 0 { \ displaystyle e ^ { i \ pi } + 1 = 0 \, }

Thế kỉ 19[sửa|sửa mã nguồn]

Xuyên suốt thế kỉ 19 toán học nhanh gọn trở nên trừu tượng. Trong thế kỉ này đã sống một trong những nhà toán học vĩ đại nhất mọi thời đại, Carl Friedrich Gauss ( 1777 – 1855 ). Không kể đến rất nhiều góp sức cho khoa học, trong toán học kim chỉ nan ông đã làm nên những khu công trình có tính cách mạng về hàm số với biến phức trong hình học và về sự quy tụ của những chuỗi. Ông đã đưa ra chứng tỏ tiên phong của định lý cơ bản của đại số và của luật tương hỗ bậc hai .Thế kỉ này tận mắt chứng kiến sự tăng trưởng của hai dạng hình học phi Euclid, trong đó tiên đề về đường thẳng song song của hình học Euclid không còn đúng nữa. Trong hình học Euclid, cho một đường thẳng và một điểm không nằm trên đường thẳng đó, thì chỉ có một và chỉ một đường thẳng song song với đường thẳng đã cho và đi qua điểm đó mà thôi .

• Lobachevsky
• Janos Bolyai
• Riemann

Nhà toán học Nga Nikolai Ivanovich Lobachevsky và đối thủ cạnh tranh của ông, nhà toán học Hungary Janos Bolyai, độc lập với nhau sáng lập ra hình học hyperbolic, trong đó sự duy nhất của những đường thẳng song song không còn đúng nữa, mà qua một điểm ngoài đường thẳng hoàn toàn có thể kẻ được vô số đường thẳng song song với đường thẳng đã cho. Trong hình học này tổng những góc của một tam giác hoàn toàn có thể nhỏ hơn 180 ° .

Hình học Hyperbolic của Lobachevsky
Hình học cổ điển Euclid
Hình học EllipticCác hình học mới Open thế kỷ 19 : Hình học Hyperbolic của LobachevskyHình học cổ xưa EuclidHình học EllipticHình học Elliptic đã được tăng trưởng sau đó vào thế kỉ 19 bởi nhà toán học người Đức Bernhard Riemann ; ở đây không hề tìm thấy đường thẳng song song và tổng những góc của một tam giác hoàn toàn có thể lớn hơn 180 °. Riemann cũng tăng trưởng hình học Riemann, trong đó hợp nhất và tổng quát hóa cao độ ba loại hình học, và ông định nghĩa khái niệm một đa tạp, trong đó tổng quát hóa khái niệm về đường và mặt. Các khái niệm này rất quan trọng trong Thuyết tương đối của Albert Einstein .Cũng trong thế kỉ 19 William Rowan Hamilton đã tăng trưởng noncommutative algebra, nền móng của triết lý vòng .Thêm vào những hướng mới trong toán học, những nền toán học cũ hơn được đưa vào những nền tảng logic mạnh hơn, đặc biệt quan trọng là trong trường hợp của giải tích với những khu công trình của Augustin Louis Cauchy và Karl Weierstrass .

• William Rowan Hamilton
• Cauchy
• Karl Weierstrass

Một dạng đại số mới được tăng trưởng vào thế kỉ 19 gọi là Đại số Boole, được phát minh bởi nhà toán học người Anh George Boole. Nó là một hệ chỉ gồm những số 0 và 1, một hệ mà ngày này có những ứng dụng quan trọng trong khoa học máy tính .

• Niels Henrik Abel
• Évariste Galois

Cũng lần đầu tiên, các giới hạn của toán học đã được khám phá. Niels Henrik Abel, một người Na Uy, và Évariste Galois, một người Pháp, đã chứng minh được rằng không có phương pháp đại số để giải phương trình đại số với bậc lớn hơn bốn. Các nhà toán học thế kỉ 19 khác áp dụng kết quả này trong chứng minh của họ rằng thước kẻ và compa là không đủ để chia ba một góc, để dựng cạnh của một hình lập phương mà thể tích của nó gấp đôi thể tích một hình lập phương cho trước, hay để dựng một hình vuông có diện tích bằng diện tích hình tròn cho trước (còn gọi là phép cầu phương hình tròn). Các nhà toán học đã tốn công vô ích để giải tất cả các bài toán này từ thời Hy Lạp cổ đại.

Các nghiên cứu và điều tra của Abel và Galois về nghiệm của rất nhiều loại phương trình đa thức khác nhau đã đặt nền móng cho những tăng trưởng sâu hơn về kim chỉ nan nhóm, và những nghành nghề dịch vụ tương quan của đại số trừu tượng. Trong thế kỉ 20 những nhà vật lý va những nhà khoa học khác đã thấy kim chỉ nan nhóm là một cách lý tưởng để nghiên cứu và điều tra symmetry .Thế kỉ 19 cũng tận mắt chứng kiến sự xây dựng của những hội toán học tiên phong : Hội toán học London vào năm 1865, Hội toán học Pháp vào năm 1872, Hội toán học Palermo vào năm 1884, Hội toán học Edinburgh vào năm 1864 và Hội toán học Mỹ vào năm 1888 .Trước thế kỉ 20, có rất ít những nhà toán học thật sự phát minh sáng tạo trên quốc tế ở bất kể thời gian nào. Phần lớn vì những nhà toán học hoặc sinh ra trong mái ấm gia đình phong phú, như Napier, hoặc được hậu thuẫn bởi những nhân vật giàu sang, như Gauss. Có rất ít người cảm thấy đời sống nghèo nàn dạy học ở trường ĐH, như Fourier. Niels Henrik Abel, không hề nhận được một vị trí nào, đã chết với gia tài là sự suy dinh dưỡng .

Thế kỉ 20[sửa|sửa mã nguồn]

David HilbertTính chuyên nghiệp của nhà toán học ngày càng trở nên quan trọng vào thế kỉ 20. Mỗi năm, hàng trăm bằng tiến sỹ trong toán học được trao, và những ngành nghề đều có trong giảng dạy và công nghiệp. Phát triển toán học đã tăng với một vận tốc cực nhanh, với quá nhiều tăng trưởng mới về khảo sát để thậm chí còn động chạm tới hầu hết những nghành nghề dịch vụ quan trọng nhất .

Vào 1900, David Hilbert đưa ra danh sách 23 bài toán chưa có lời giải trong toán học tại Hội nghị các nhà toán học quốc tế. Các bài toán này bao trùm rất nhiều lĩnh vực của toán học và đã tạo nên sự chú ý đặc biệt trong toán học thế kỉ 20. Hiện nay mười bài toán đã có lời giải, bảy đã giải được một phần và hai bài vẫn còn mở. Bốn bài còn lại quá lỏng để nói rằng liệu đã giải được chưa. Hilbert cũng đã đặt nền móng cho việc tiên đề hóa hình học với cuốn sách “Grundlagen der Geometrie” (Nền tảng của Hình học) bao gồm 21 tiên đề, thay cho các tiên đề Euclid truyền thống. Chúng tránh đi những điểm yếu đã được chỉ ra trong các tiên đề Euclid, mà các tác phẩm của ông (Euclid) lúc đó vẫn được xem như sách giáo khoa. Ông mong muốn hệ thống hóa toán học trên một nền tảng logic vững chắc và đầy đủ, tin rằng:

1. Tất cả toán học có thể suy ra từ một hệ thống hữu hạn các tiên đề được chọn ra một cách đúng đắn
2. Rằng một hệ thống tiên đề như vậy là có thể chứng minh được tính nhất quán (tính không mâu thuẫn) của nó

Cũng chính Hilbert đã đưa ra khái niệm khoảng trống Hilbert, một cơ sở cho giải tích hàm .
Kurt Gödel

Những năm 1930, Kurt Gödel đã đưa ra định lý bất toàn (Gödel’s incompleteness theorems) khẳng định rằng bất kì một hệ tiên đề hình thức độc lập nào đủ mạnh để miêu tả số học cũng hàm chứa những mệnh đề không thể khẳng định mà cũng không thể phủ định; tính nhất quán của một hệ thống tiên đề không thể được chứng minh bên trong hệ thống đó. Mở rộng ra, không thể đi tìm tính chân lý của toán học (và của khoa học nói chung) bên trong cấu trúc duy lý của bản thân toán học hay của khoa học đó; cái đúng của toán học phải tìm ngoài toán học.

Trong những năm 1900, Srinivasa Aiyangar Ramanujan (1887-1920) đã phát triển hơn 3000 định lý, bao gồm lý thuyết về tính chất của các siêu hợp số (highly composite number), hàm phần chia (partition function) và các tiệm cận của nó, rồi các hàm theta Ramanujan. Ông cũng tạo nên những đột phá và phát hiện trong lĩnh vực hàm gamma, dạng modular, chuỗi phân kì, chuỗi siêu hình học và lý thuyết số nguyên tố.

Năm 1947, tác phẩm ” Cơ sở nghiên cứu và phân tích kinh tế tài chính ” của Paul Samuelson công bố được xem là khởi đầu của toán kinh tế tài chính đương đại. [ 38 ]Năm 1952, Sir John Anthony Pople ( 31/10/1925 – 15/3/2004 ) nhà hóa học người Anh tại ĐH Cambridge đã vận dụng toán học trong hóa học, lập ra công thức cho một sơ đồ cơ bản để tăng trưởng những quy mô toán học Giao hàng nghiên cứu và điều tra phân tử mà không cần triển khai thí nghiệm. Ông đã sử dụng máy tính ship hàng cho việc kiểm tra và xác lập cấu trúc hóa học cũng như những cụ thể của vật chất. Walter Kohn người Áo ( 9/3/1923 – 19/4/2016 ), thao tác tại ĐH Santa Barbara ( Mỹ ) người điều tra và nghiên cứu kim chỉ nan về tỷ lệ, đã đơn giản hóa miêu tả toán học về sự link giữa những nguyên tử tạo nên phân tử .

Những năm 60-70 của thế kỷ 20, việc giáo dục toán học đã bắt đầu sử dụng các phương pháp mới, trong đó nghiên cứu toán được bắt đầu từ những lĩnh vực cơ sở như lý thuyết tập hợp, logic sơ cấp, hệ thống số và hệ thống đếm, số học đồng nhất mô-đun (modular consistency arithmetic).[39]

Các phỏng đoán nổi tiếng trong quá khứ tạo nên những kĩ thuật mới và mạnh. Wolfgang Haken và Kenneth Appel đã sử dụng một chiếc máy tính để chứng tỏ định lý bốn màu vào năm 1976. [ 40 ]
Andrew Wiles, thao tác một mình trong văn phòng trong nhiều năm trời, sau cuối đã chứng tỏ được Định lý lớn Fermat vào năm 1995, kết thúc hơn 300 năm đi tìm giải thuật .Toàn bộ những nghành nghề dịch vụ mới của toán học như logic toán, topo học, kim chỉ nan độ phức tạp, và triết lý game show đã đổi khác những thể loại thắc mắc mà hoàn toàn có thể vấn đáp được bởi những giải pháp toán học .

Nhóm Bourbaki của Pháp đã cố gắng đưa toàn bộ toán học thành một thể thống nhất chung, xuất bản dưới bút danh Nicolas Bourbaki. Công trình khổng lồ của họ đã gây rất nhiều tranh luận trong giáo dục toán học.

Đến cuối thế kỉ, toán học đã thậm chí còn xâm nhập vào thẩm mỹ và nghệ thuật, như hình học fractal đã tạo nên những hình thù xinh xắn chưa từng thấy khi nào .

Thế kỉ 21[sửa|sửa mã nguồn]

Vào buổi bình minh của thế kỉ 21, rất nhiều nhà giáo dục đã bày tỏ quan ngại về một lớp người nghèo, không được học tập về toán học và khoa học. [ 41 ] Trong khi đó toán học, khoa học, công trình sư và công nghệ tiên tiến đã cùng nhau tạo nên những tri thức, liên kết, và gia tài mà những triết gia cổ đại không dám mơ đến .Năm 2005, Peter David Lax ( 1/5/1926, Viện Khoa học Toán Courant, Đại học Thành Phố New York ) đã nghiên cứu và điều tra thành công xuất sắc triết lý và ứng dụng của phương trình vi phân riêng phần cũng như giám sát nghiệm của chúng .Vào giữa tháng 3 năm 2007, một đội những nhà nghiên cứu khắp Bắc Mĩ và châu Âu đã sử dụng những mạng máy tính để vẽ sơ đồ E8 thuộc nhóm Lie. [ 42 ] Mặc dù ta chưa thể biết đúng chuẩn việc này có ứng dụng gì, nhưng tò mò này lưu lại một mốc quan trọng về cả ý thức hợp tác và công nghệ tiên tiến máy tính trong toán học văn minh, khi kiến thiết xây dựng quy mô vật thể phức tạp nhất mà con người từng biết đến với 248 chiều, với dung tích bộc lộ lớn hơn cả bộ gen con người. [ 43 ]

• Cấu trúc E8 hai chiều, triển khai bởi Peter McMullen
• E8 ba chiều
• 

  E8

  Xem thêm: IIS 8.5 Detailed Error – 404.0

Những yếu tố toán học còn chờ đón trong tương lai[sửa|sửa mã nguồn]

Bảy bài toán thiên niên kỷ[sửa|sửa mã nguồn]

Ngày 24/5/2000, Viện Toán học Clay công bố list bảy bài toán chưa giải được với phần thưởng cho việc xử lý mấu chốt trong việc giải mỗi bài là 1 triệu đô la Mỹ : [ 44 ]

Các bài toán của Hilbert[sửa|sửa mã nguồn]

23 bài toán được nhà toán học người Đức David Hilbert đưa ra trong Hội nghị Quốc tế về Toán học (International Congress of Mathematicians ICM) lần thứ hai năm 1900 tại Paris, trong đó một số đã được giải quyết trong thế kỷ 20.[45]

Liên kết ngoài[sửa|sửa mã nguồn]

Tiếng quốc tế[sửa|sửa mã nguồn]

Source: https://mix166.vn
Category: Công Nghệ