Một số thủ thuật máy tính CASIO fx-580VN X – Nhut Nguyen Minh
- Thủ thuật chia đa thức một biến thường được sử dụng hỗ trợ thủ thuật giải phương trình bậc cao
- Thủ thuật nhập hàm cot và arccot thường được sử dụng hỗ trợ thủ thuật giải phương trình lượng giác
Mỗi ngày biết thêm một thủ thuật dù là nhỏ nhất, đơn thuần nhất nhưng khi bạn đủ sức phối hợp lại thì đó sẽ là những thủ thuật, những kỹ năng và kiến thức tuyệt vời
Mục lục bài viết
1 Chia đa thức một biến
Máy tính CASIO fx-580VN X không có tính năng tìm thương và dư trong phép chia đa thức một biến nhưng nếu biết cách tất cả chúng ta vẫn hoàn toàn có thể tìm được
Chú ý 1
Thủ thuật này chỉ vận dụng với phép chia hết
Bước 1 Nhấn phím ![]()
Bước 2 Nhập biểu thức bị chia f(x)
Bước 3 Nhấn phím ![]()
Bước 4 Nhập biểu thức chia g(x)
Bước 5 Nhấn phím CALC
Bước 6 Nhập ![]()
Bước 7 Nhấn phím =
Bước 8 Phân tích theo các hướng dẫn Khai triển đa thức một biến bằng máy tính Casio fx-580VN X để tìm thương
Thủ thuật này thường được sử dụng khi giải phương trình bậc cao, xác lập nghiệm của phương trình là nghiệm đơn hay nghiệm bội, …
Ví dụ 1
Giải phương trình ![]()
Bước 1 Sử dụng tính năng SOLVE tìm nghiệm thứ nhất
Suy ra ![]() là nghiệm thứ nhất
là nghiệm thứ nhất
Phương trình đã cho là phương trình đa thức bậc năm và tất cả chúng ta đã tìm được một nghiệm
Phương pháp tối ưu nhất là phân tích ![]() thành
thành ![]()
Dễ thấy 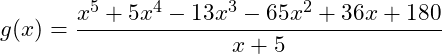
Bước 2 Tìm đa thức g(x)
- Bước 2.1 Nhấn phím

- Bước 2.2 Nhập đa thức

- Bước 2.3 Nhấn phím
- Bước 2.4 Nhập đa thức
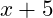

- Bước 2.5 Nhấn phím CALC

- Bước 2.6 Nhập

- Bước 2.7 Nhấn phím =

- Bước 2.8 Suy ra đa thức
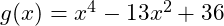
Bước 3 Sử dụng phương thức tính toán Equation/ Func giải phương trình ![]()
![]()
![]()
![]()
Vậy tập nghiệm của phương trình đã cho là ![]()
2 Hàm số lượng giác cot và hàm số lượng giác ngược arccot
Vì máy tính CASIO fx-580VN X không thiết kế phím ![]() và phím
và phím ![]() nên chúng ta sẽ nhập gián tiếp thông qua phím
nên chúng ta sẽ nhập gián tiếp thông qua phím ![]() và phím
và phím ![]()
- Nhập
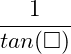 hoặc
hoặc 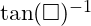 để nhập hàm cot
để nhập hàm cot - Nhập
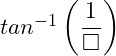 hoặc
hoặc 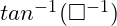 để nhập hàm arccot
để nhập hàm arccot
Thủ thuật này thường được sử dụng khi tính giá trị lượng giác của một góc, giải phương trình lượng giác, …
Ví dụ 2.1
Tính giá trị lượng giác của góc ![]()
- Cách 1 Dựa vào phím và phím

- Cách 2 Dựa vào phím và phím
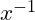

Ví dụ 2.2
Giải phương trình 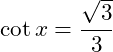
- Cách 1 Dựa vào phím và phím

Vậy nghiệm của phương trình đã cho là ![]() với
với ![]()
- Cách 2 Dựa vào phím và phím

Vậy nghiệm của phương trình đã cho là với
Chú ý 2
Vị trí của dấu ![]() và
và ![]() cần được đặt chính xác
cần được đặt chính xác
3 Hiển thị kết quả tính toán thập phân
Với các thiết lập mặc định, máy tính CASIO fx-580VN X sẽ “ cố gắng nỗ lực ” hiển thị hiệu quả thống kê giám sát dưới dạng phân số, căn thức
Tuy nhiên trong một số ít trường hợp đặc biệt quan trọng tất cả chúng ta cũng cần hiển thị tác dụng thống kê giám sát dưới dạng thập phân
Phương pháp 1 Thiết lập cấu hình Input/ Output
Bước 1 Nhấn phím SETUP

Bước 2 Chọn Input/ Output

Bước 3 Chọn MathI/ DecimalO

Phương pháp 2 Sử dụng phím ![]()
Phương pháp 3 Sử dụng phím ![]()
Chú ý 3Phương pháp 1 chỉ nên sử dụng trong một số ít trường hợp rất đặc biệt quan trọng
Thủ thuật này thường được sử dụng khi lập bảng xét dấu, bảng biến thiên bằng, …
Ví dụ 3
Lập bảng biến thiên của hàm số ![]()
Bước 1 Tập xác định ![]()
Bước 2 ![]()
Bước 3 Giải phương trình ![]()
Bước 4 Lập bảng biến thiên
Chắc các bạn cũng biết chúng ta cần sắp xếp các giá trị làm cho hàm số f(x) không xác định hoặc ![]() theo thứ tự tăng dần
theo thứ tự tăng dần
Nói như vậy có nghĩa bạn cần xác định nghiệm ![]() và
và ![]() nghiệm nào nhỏ, nghiệm nào lớn
nghiệm nào nhỏ, nghiệm nào lớn
Phương pháp đơn thuần nhất và hiệu suất cao nhất trong trường hợp này là sử dụng phím
Suy ra nhỏ hơn

4 Nhập giá trị âm trong phương thức tính toán Table
Phương thức đo lường và thống kê Table trong máy tính CASIO fx-580VN X có nhiều tăng cấp đáng kể
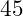 dòng giá trị với một hàm f(x) và
dòng giá trị với một hàm f(x) và 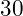 dòng với hai hàm f(x) và g(x)
dòng với hai hàm f(x) và g(x)- Cho phép nhập phép tính đạo hàm và phép tính tích phân
- Cho phép chỉnh sửa trực giá trị của
- Khi nhấn phím
 hoặc
hoặc  thì bảng giá trị sẽ tự động thay đổi
thì bảng giá trị sẽ tự động thay đổi
Nhờ những nâng đáng kể này mà phương pháp giám sát Table có rất nhiều ứng dụng thiết thực, đặc biệt quan trọng là trong Kỳ thi Trung học Phổ thông Quốc gia
Ở đây mình sẽ hướng dẫn các bạn khai thác nâng cấp cho phép chỉnh sửa trực giá trị để kiểm tra giá trị nào là nghiệm của phương trình
Ví dụ 4
Nghiệm của phương trình ![]() là
là
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Vì nghiệm của phương trình đã được cho trước nên tất cả chúng ta sẽ sử dụng tính năng CALC hoặc phương pháp đo lường và thống kê Table để kiểm tra
Phương pháp hiệu suất cao nhất trong trường hợp này là sử dụng phương pháp giám sát Table
Bước 1 Nhập biểu thức f(x) bằng ![]()

Bước 2 Nhập ![]()
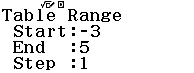
Bước 3 Nhấn phím =
Quan sát bảng giá trị dễ thấy giải pháp D là đáp án
Giả sử chúng ta cần nhập giá trị ![]() để kiểm tra thì chúng ta sẽ nhập
để kiểm tra thì chúng ta sẽ nhập 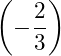
Tổng quát để nhập trực tiếp một giá trị âm trong phương thức tính toán Table chúng ta sẽ nhập ![]() với
với ![]()
5 Xử lí kết quả tính toán tràn màn hình
Giả sử chúng ta có kết quả tính toán ![]() tràn màn hình
tràn màn hình
Bước 1 Nhấn phím
Bước 2
- Nếu chữ số
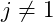 thì chúng ta sẽ nhập
thì chúng ta sẽ nhập 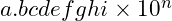
- Nếu chữ số
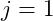 thì chúng ta sẽ nhập
thì chúng ta sẽ nhập 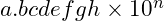
Bước 3 Nhấn phím ![]()
Chú ý 5
- Nếu chữ số cuối cùng sau khi xử lí là chữ số
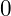 thì chúng ta cần kiểm tra cẩn thận lại
thì chúng ta cần kiểm tra cẩn thận lại - Số mũ tối đa là có thể áp dụng thủ thuật này là
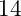
- Giá trị có
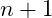 chữ số
chữ số
Thủ thuật này thường được sử dụng khi tìm ước chung lớn nhất, bội chung nhỏ nhất, khai triển đa thức một biến, lập tam giác Pascal, …
Ví dụ 5
Khai triển đa thức ![]()
Bước 1 Nhập đa thức ![]()

Bước 2 Nhấn phím CALC => nhập => nhấn phím =

Bước 3 Xử lí kết quả tràn màn hình ![]()
Suy ra ![]()
Bước 4 Phân tích ![]() theo chiều từ phải sang trái
theo chiều từ phải sang trái
- được phân tích thành
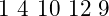
- Dự đoán
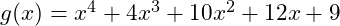
Bước 5 Kiểm tra đa thức g(x)

Vậy ![]()
6 Rút gọn biểu thức có chứa căn thức
Rút gọn biểu thức chứa căn thức nói chung căn bậc hai, căn bậc ba nói riêng là dạng toán thường gặp trong chương trình Toán 9
Dạng toán này tuy không khó nhưng nếu kĩ năng nghiên cứu và phân tích chưa tốt thì việc rút gọn tốn khá nhiều thời hạn
Ở đây mình sẽ hướng dẫn các bạn hai phương pháp giúp rút gọn nhanh biểu thức có dạng ![]()
Phương pháp 1 Dựa vào phương thức tính toán Equation/ Func
Bước 1 Giải phương trình 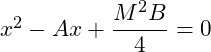
Bước 2 Tìm được nghiệm và
Vậy ![]()
Phương pháp 2 Dựa vào tính năng SOLVE và tính năng CALC
Bước 1 Nhập biểu thức ![]()
Bước 2 Nhấn phím SOLVE
Bước 3 Nhập ![]()
Bước 4 Nhấn phím =
Bước 5 Nhấn phím =
Chú ý 6.1
- Biểu thức đầu vào là biểu thức hai biến nhưng ta đã gán cho biến một giá trị cụ thể nên hiện tại biểu thức đã trở thành biểu thức một biến (biến
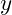 )
) - Thuật giải này sẽ dừng khi là số nguyên
Ví dụ 6.1
Rút gọn biểu thức ![]()
Phương pháp 1 Dựa vào phương thức tính toán Equation/ Func
Bước 1 Giải phương trình 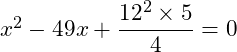
Bước 2 Tìm được nghiệm và ![]()
Vậy ![]()
Phương pháp 2 Dựa vào tính năng SOLVE và tính năng CALC
Bước 1 Nhập biểu thức ![]()

Bước 2 Nhấn phím SOLVE

Bước 3 Nhập ![]()

Bước 4 Nhấn phím =

Bước 5 Nhấn phím =

Với ![]() thì
thì ![]() không thỏa thủ thuật
không thỏa thủ thuật
Bước 6 Nhấn phím SOLVE => nhấn phím => nhập => nhấn phím => nhấn phím

Với ![]() thì
thì ![]() thỏa thủ thuật
thỏa thủ thuật
Vậy ![]()
Chú ý 6.2
- Phương pháp 1 có thể rút gọn được mọi biểu thức có dạng
- Phương pháp 2 có thể không rút gọn được ở một số biểu thức tuy nhiên Phương pháp 2 có thể được sử dụng với căn bậc ba
Ví dụ 6.2
Rút gọn biểu thức ![]()
Bước 1 Nhập biểu thức ![]()

Bước 2 …
Vậy ![]()
7 Màn hình hiển thị nhiều dòng
Bước 1 Nhấn phím SETUP
Bước 2 Chọn Input/ Output
Bước 3 Chọn LineI/ LineO

Thủ thuật này thường được sử dụng để hỗ trợ thủ thuật xử lí hiệu quả đo lường và thống kê tràn màn hình hiển thị
Quan sát lại thủ thuật xử lí tác dụng đo lường và thống kê tràn màn hình hiển thị, dễ thấy ngay khi nhấn phím hiệu quả đo lường và thống kê sẽ biến mất
Lúc bấy giờ bạn cần ghi nhớ tác dụng đo lường và thống kê trong đầu hoặc ghi ra giấy ( hoàn toàn có thể quên hoặc sai sót )
Nhưng nếu bạn đã thiết lập màn hình hiển thị hiển thị nhiều dòng thì khi nhấn phím hiệu quả sẽ không biến mất nữa

Chú ý 7Thiết lập tùy chọn MathI / MathO là mặc định ngay khi sử dụng xong thủ thuật
8 Tìm phương trình bậc hai khi biết trước một nghiệm
Chú ý 8Chọn phương pháp thống kê giám sát Table và thiết lập sử dụng một hàm f ( x ) trước khi triển khai thủ thuật
Giả sử ![]() là nghiệm của một phương trình bậc hai
là nghiệm của một phương trình bậc hai
Bước 1 Nhập biểu thức ![]()

Bước 2 Nhập ![]()

Bước 3 Nhấn phím =

Tìm những giá trị sao cho f(x) có giá trị nguyên, giả sử ![]() có giá trị nguyên khi đó phương trình bậc hai cần tìm là
có giá trị nguyên khi đó phương trình bậc hai cần tìm là ![]()
Thủ thuật này thường được sử dụng khi giải phương trình ( đặc biệt quan trọng là phương trình căn thức ) bằng tính năng SOLVE
Ví dụ 8
Tìm một nghiệm của phương trình ![]()
Bước 1 Tìm nghiệm phương trình ![]()
Bước 2 Gán nghiệm vừa tìm được vào biến nhớ

Bước 3 Biểu diễn dưới dạng căn thức
Bước 3.1 Nhập biểu thức
Bước 3.2 Nhập
Bước 3.3 Nhấn phím =

Quan sát bảng giá trị dễ thấy ![]() suy ra phương trình bậc hai cần tìm là
suy ra phương trình bậc hai cần tìm là ![]()
Bước 3.4 Giải phương trình ![]()
Suy ra ![]()
Vậy phương trình đã cho có một nghiệm là ![]()
9 Vấn đề nghiệm “xấu” khi giải phương trình đa thức
Có 1 số ít trường hợp khi giải phương trình bậc ba hoặc bậc bốn bằng phương pháp giám sát Equation / Func máy tính sẽ hiển thị nghiệm dưới dạng thập phân, không hiển thị được dưới dạng căn thức
Đây thực sự là một hạn chế khá lớn, thủ thuật này sẽ giúp bạn xử lý phần nào hạn chế trên
9.1 Phương trình bậc ba
Ví dụ 9.1
Giải phương trình ![]()
Bước 1 Giải phương trình
Suy ra phương trình đã cho có ba nghiệm
Trong ba nghiệm tìm được chỉ có nghiệm là hoàn toàn có thể sử dụng ngay, muốn sử dụng được hai nghiệm còn lại tất cả chúng ta cần màn biểu diễn nó dưới dạng căn thức
Dễ thấy chúng là nghiệm của một phương trình bậc hai, dưới đây là hai chiêu thức tìm ra phương trình bậc hai này
Phương pháp 1 Sử dụng thủ thuật chia đa thức một biến

Suy ra phương trình bậc hai cần tìm là ![]()
Chú ý 9.1Phương pháp này chỉ khả dụng khi có tối thiểu một nghiệm là số nguyên
Phương pháp 2 Sử dụng định lý Viète
Bước 1 Gán nghiệm vào biến nhớ, nghiệm ![]() vào biến nhớ
vào biến nhớ ![]()
Bước 2 Chọn phương pháp đo lường và thống kê Complex

Bước 3 Nhập đa biểu thức ![]()

Bước 4 Nhấn phím =
Suy ra phương trình bậc hai cần tìm là
Khi đã tìm được phương trình bậc hai thì yếu tố gần như đã được xử lý xong, việc làm ở đầu cuối là giải phương trình bậc hai vừa tìm được
Vậy tập nghiệm của phương trình đã cho là ![]()
9.2 Phương trình bậc bốn
Ví dụ 9.2.1
Giải phương trình ![]()
Bước 1 Giải phương trình
Bước 2 Gán ![]() lần lượt vào các biến nhớ A, B, C, D
lần lượt vào các biến nhớ A, B, C, D
Bước 3 Chọn phương pháp thống kê giám sát Complex
Bước 4 Nhập đa biểu thức ![]()

Bước 5 Nhấn phím =
Suy ra hai phương trình bậc hai cần tìm là ![]() và
và ![]()
Bước 6 Giải phương trình
Bước 7 Giải phương trình
Vậy bốn nghiệm của phương trình đã cho là ![]() ,
, ![]() ,
, ![]() ,
, ![]()
Ví dụ 9.2.2
Giải phương trình ![]()
Bước 1 Giải phương trình
Bước 2 Gán lần lượt vào các biến nhớ A, B, C, D
Bước 3 Chọn phương pháp thống kê giám sát Complex
Bước 4 Nhập đa biểu thức ![]()

Vì không hề nhìn thấy nghiệm nào với nghiệm nào là nghiệm của một phương trình bậc hai nên cần kiểm tra trải qua đa biểu thức trên
Bước 5 Nhấn phím =
Suy ra và ![]() là nghiệm của một phương trình bậc hai, và cũng là nghiệm của một phương trình bậc hai
là nghiệm của một phương trình bậc hai, và cũng là nghiệm của một phương trình bậc hai
Bước 6 Nhập đa biểu thức ![]()

Bước 7 Nhấn phím =
Suy ra hai phương trình bậc hai cần tìm là và
Bước 8 Giải phương trình
Bước 9 Giải phương trình
Vậy bốn nghiệm của phương trình đã cho là, , ![]() ,
, ![]()
Không phải phương trình bậc ba, bậc bốn nào cũng hoàn toàn có thể xử lý bằng thủ thuật này
Trường hợp không xử lý được bạn hoàn toàn có thể sử dụng dịch vụ trực tuyến WolframAlpha hoặc kỹ năng và kiến thức Toán học
- Đối với phương trình bậc ba bạn có thể sử dụng phương pháp được công bố bởi Gerolamo Cardano
- Đối với phương trình bậc bốn bạn có thể sử dụng phương pháp của Ferrari
Source: https://mix166.vn
Category: Thủ Thuật


































































